Dear lammps-users,
I am trying to compute the Radial Distribution Function (RDF) for liquid Si by using Tersoff potential (Tersoff, Phys Rev B, 38, 9902 (1988)) but I am not getting the correct peak width and shape. Here is my code:
###################################Code################################
units real
dimension 3
boundary p p p
atom_style charge
lattice diamond 5.2763
region box block 0 1 0 1 0 1 units lattice
create_box 1 box
create_atoms 1 box
replicate 5 5 5
mass * 27.9861
pair_style tersoff
pair_coeff * * …/…/…/…/…/…/…/…/potentials/Si2.tersoff Si
#pair_style lj/cut 8.0
#pair_coeff * * 1 1 8.0
#compute myrdf all rdf 100 1 1
#fix 4 all ave/time 1 1 1 c_myrdf file tersoff2_3000Kl.rdf mode vector
#rerun dump2_tersoff2_nvt3000.dump first 30000 every 10 stop 50000 dump x y z
compute eng all pe/atom
compute eatoms all reduce sum c_eng
reset_timestep 0
thermo 10
thermo_style custom step pe density temp etotal
min_style sd
minimize 1e-10 1e-10 5000 10000
fix 2 all box/relax iso 0.0 vmax 0.001
min_style sd
minimize 1e-10 1e-10 5000 10000
unfix 2
dump 1 all atom 10 dump2_tersoff2_nvt3000.dump
timestep 0.01
fix 3 all nvt temp 3000.0 3000.0 1.0
run_style verlet
run 50000
###################################End###########################
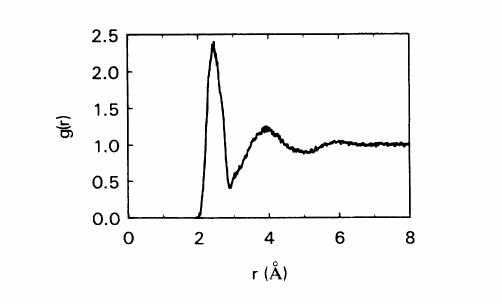
RDF was calculated by running the code second time with changing the pair style, uncommenting all the lines for rerun command and deleting/commenting everything below the rerun line. Final RDF was computed as the average of the data between 30000 and 45000 timesteps .
I have attached the RDF thus plotted, along with temperature profile and the RDF published for Tersoff potential.
Would you please let me know if I am making any mistake in making liquid Si or computing its RDF? Let me know if you have any questions in understanding the code or my problem. Any suggestion or help is highly appreciated.
Thanks for your time,
Regards,
Vishank
plot_tersoff2_3000Kl.rdf.eps (19.1 KB)
Temp_profile_3000K.pdf (31.1 KB)