Dear Alex,
thank for reply. Suppose rigid body 1 has n1 spheres and rigid body 2 has
n2. Do we really need to evaluate the distance of each sphere in body 1 to
each sphere in body 2? This operation is an O(n1 x n2) complexity.
you are not paying attention to my explanations. what you are supposing
here is *not* how LAMMPS computes interactions for rigid bodies.
also, your picture seems to imply that you are looking at only repulsive
"hard" interactions. what LAMMPS does is much smarter.
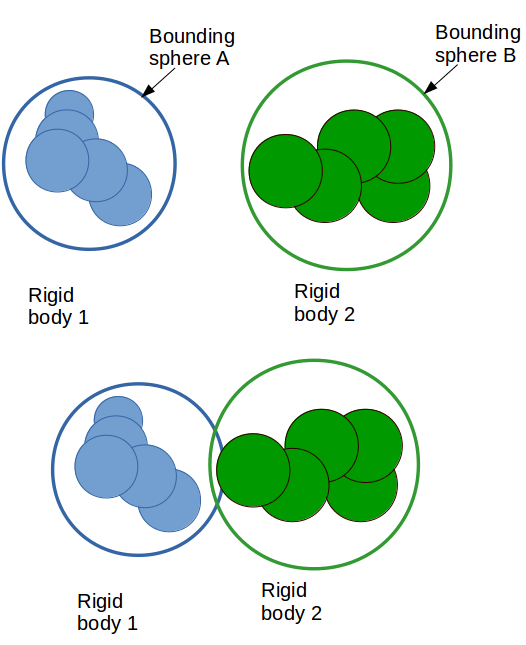
[image: BS]
As shown in the above picture, Bounding spheres (A, B) that tightly
encompass composing spheres of a rigid body are constructed
*. *
they can only be as tight as the interaction cutoff allows. for, say,
colloid particle interactions, these can be as long as 10 angstrom or more.
(1)* If A and B do not intersect, then we can skip the O(n1 x n2)
pairwise tests.*
(2) If A and B do intersect, then rigid body 1 and 2 might be colliding,
thus the O(n1 x n2) pairwise tests are needed to calculate the contact
force.
I checked the fix_rigid source codes, it seems that in Lammps the step (1)
is ignored?
as i already mentioned that is not needed. LAMMPS uses verlet lists, which
is equivalent to put those bounding spheres _around each individual
particle_.
so in your case 2 you are actually computing more interactions than what
LAMMPS will do. looking at the fix rigid code is *completely* irrelevant.
all it does is sum up forces on the constituent particles to the rigid
bodies, which is an O(N) operation. the force computation, which is for a
sufficiently large system is also an O(N) operation thanks to the verlet
lists (and generating verlet lists is O(N) as well, thanks to using binning
into cell lists). i suggest you study the original LAMMPS paper or some of
the introductory talk slides on the LAMMPS home page to see.
My understanding is that the neighbor list of a sphere in rigid body only
contains spheres in other rigid bodies, hence the number of spheres in the
list is quite low, as there are more space between angular bodies than that
of spheres assembly. The resultant contact force acting on a rigid body is
the sum of contact forces on each composing spheres, no need to do (1) and
(2) as mentioned above.
yes, this can be defined using the neigh_modify exclude command. please
keep in mind, that LAMMPS is designed to handle a large variety of systems
equally well. in my personal opinion, what LAMMPS is doing is, in fact,
superior to what you are asking for.
axel.