In method 1 there is no reason for the two thermostats to take or give the same amount of energy since they independently act on the two independent groups.
Note that sigma in pair_style lj/cut is the energy minimum. From the doc page: “Note that sigma is defined in the LJ formula as the zero-crossing distance for the potential, not as the energy minimum at 2^(1/6) sigma.”
Ray
Thanks for your email, Ray. I sort of see where you are coming from, however, there’s no physical basis for the two thermostats to supply different amounts of energy, right? Currently, I assume that the hot atoms lose heat to the cold atoms, and therefore the hot reservoir loses heat to the hot atoms, and the cold atoms lose heat to the cold reservoir. On physical grounds, I expect the amount of heat exchanged between all ‘parties’ to be the same in magnitude, even if the two thermostats are ‘unaware’ of the other. Is there a computational reason behind the discrepancy?
I also have a couple of other questions, I hope you all don’t mind me asking.
(1) When is it appropriate to use the ‘minimize’ command? I was under the (perhaps mistaken) impression that equilibration is essentially the process by which the substance arrives at its equilibrium state, so the potentials are minimised. So far, I had been equilibrating via an NVE integration (with some velocity scaling). I noticed that this would make my solids ‘shrink away’ from each other - so I just tried adding in a minimize command at the beginning - and this stopped the ‘shrinking away’.
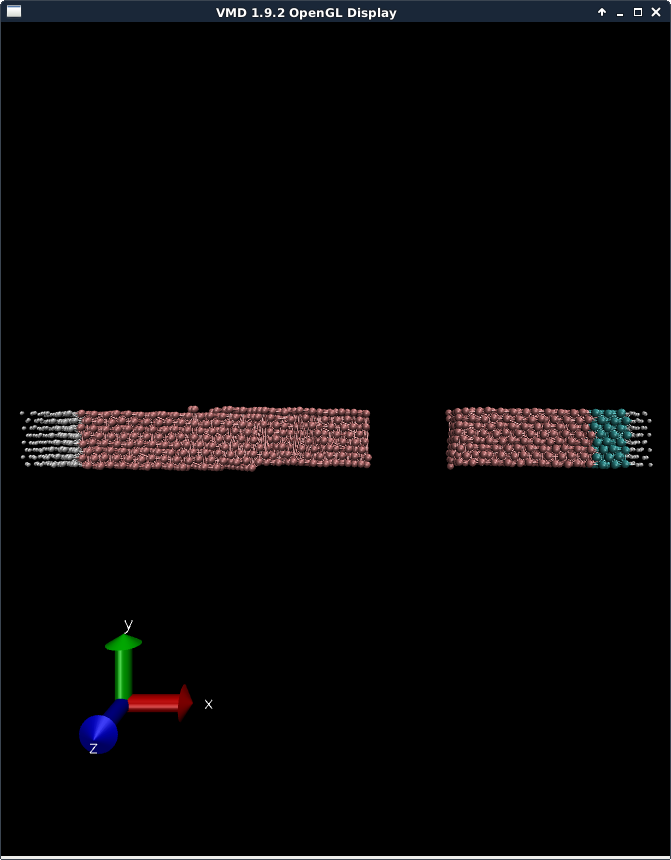
(2) Have any of you found that when modelling a solid using an LJ potential (some academic papers report using LJ for solids), that they ‘bend’ slightly? Kind of like a cantilever being pulled a bit? I realise this might be a vague question, but I noticed this in VMD, and was wondering whether anyone else has ever seen this. I’ve attached a screenshot in VMD to show you what I mean.
Thanks,
Ashim