Dear LAMMPS users,
I want to follow-up on a question that was discussed on the forum: http://lammps.sandia.gov/threads/msg34227.html
I would like to control the pressure on a non-periodic dimension using a moving harmonic wall, as suggested by Steve in the above discussion.
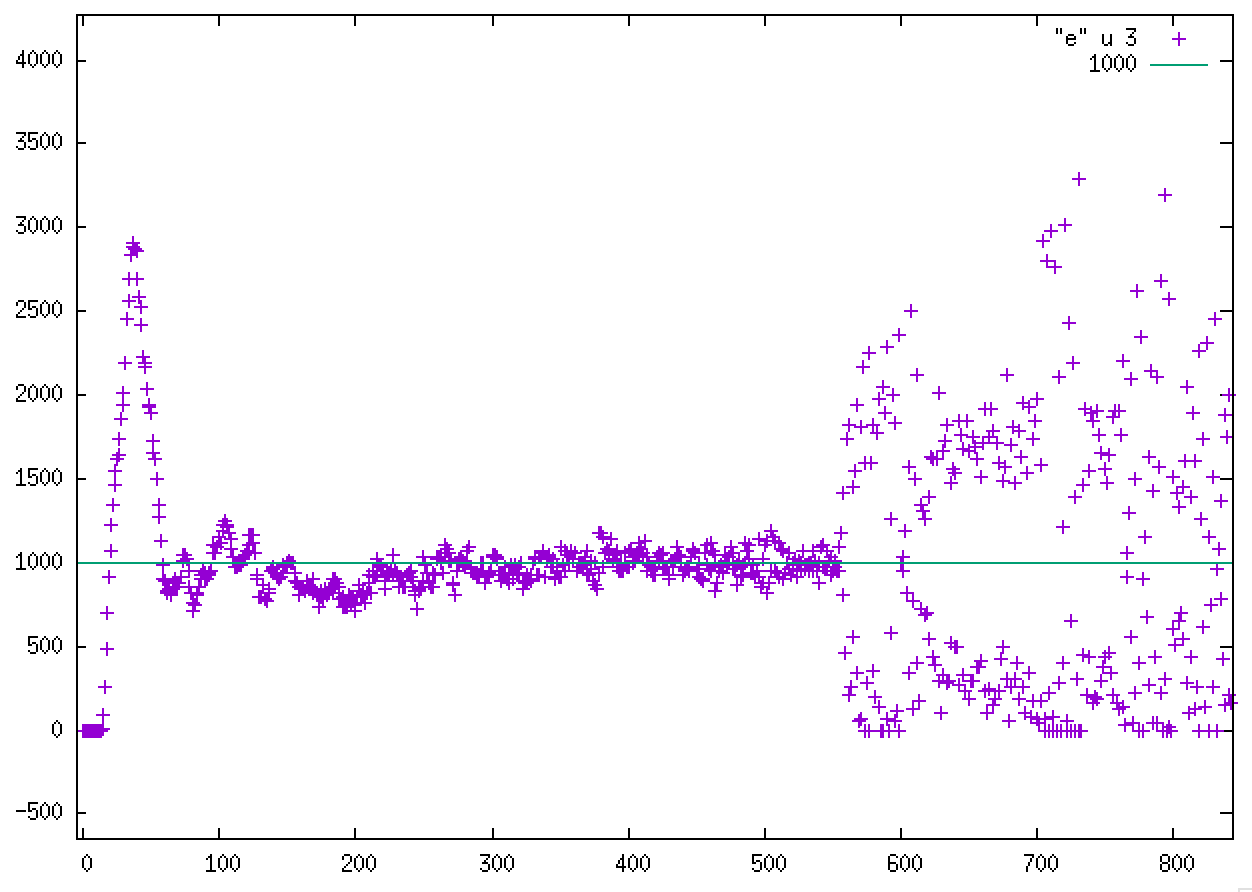
The “barostat” works for some time and then becomes chaotic and crash.
I made a toy system made of water molecules periodic in y, z but not in x where I put a harmonic wall at the position defined by the following equation (I consider only the xlo side here):
x = x0 + v*t
The velocity of the wall is a function of time and adjusted every cycle from the velocity at the previous cycle (with a loop):
v(i) = v(i-1) + gamma*dv
Gamma is given by:
gamma = (Pext - P)/Pext
with Pext the external pressure and P the actual wall pressure computed from the force on the wall via: P = 68568.415*abs(fwall)/area (in real units) and fwall is time-averaged over 10 steps corresponding to one cycle.
Everything work as expected at the beginning and the pressure equilibrates well however after ~500 cycles, the pressure starts to diverge and rapidly becomes chaotic and the simulation crash.
I would appreciate any advice to solve this.
I know there are other simulation options but I just would like to understand this behavior.
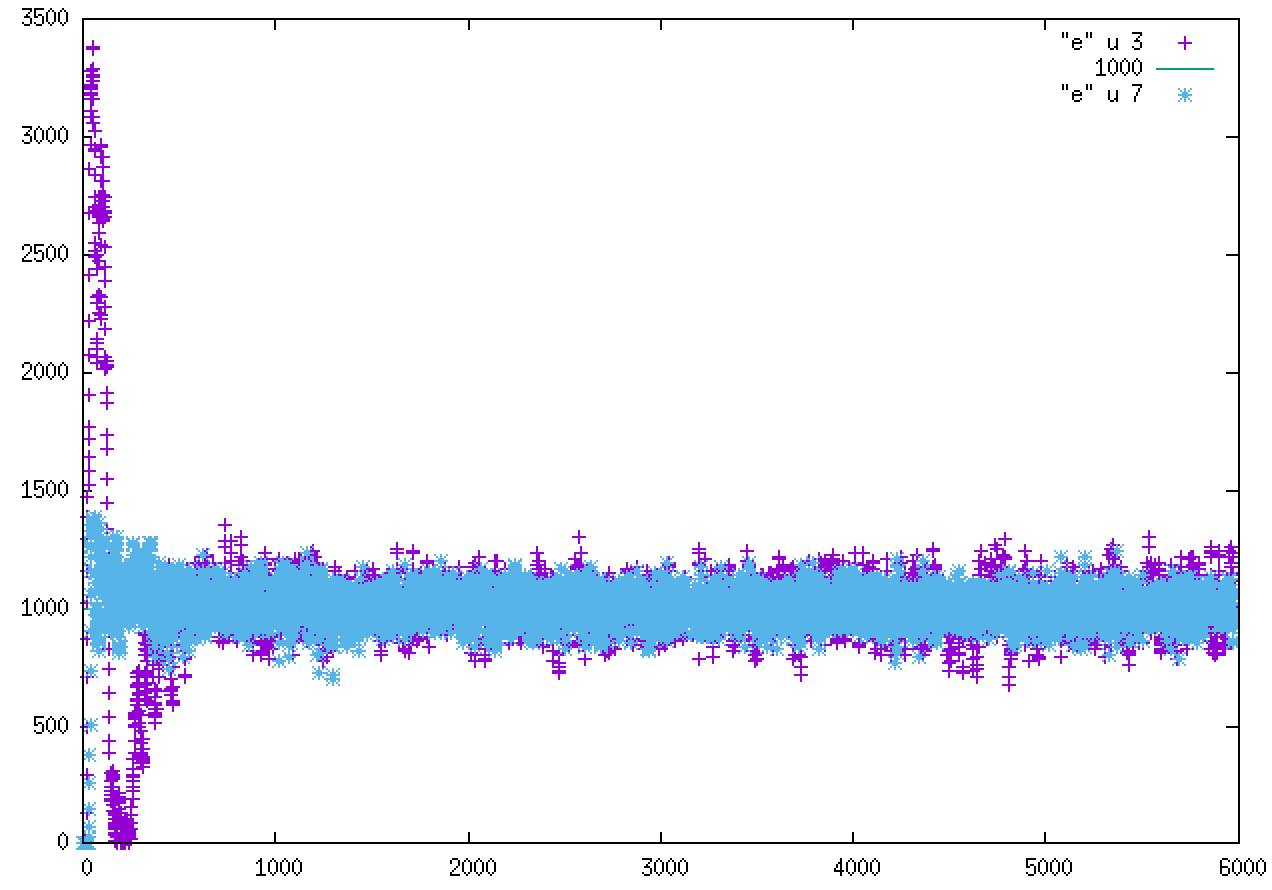
I attach a plot of the actual pressure P (Atm) as a function of cycles (10 MD steps) with Pext = 1000 Atm as well as the corresponding input, force field and data files.
I use REAX/C & LAMMPS-17Nov16.
Thank you and regards,
Nicolas
water-Pext.in (3 KB)
water.data (40 KB)
ffield (28 KB)
Dear LAMMPS users,
I want to follow-up on a question that was discussed on the forum:
http://lammps.sandia.gov/threads/msg34227.html
I would like to control the pressure on a non-periodic dimension using a
moving harmonic wall, as suggested by Steve in the above discussion.
The “barostat” works for some time and then becomes chaotic and crash.
I made a toy system made of water molecules periodic in y, z but not in x
where I put a harmonic wall at the position defined by the following
equation (I consider only the xlo side here):
x = x0 + v*t
The velocity of the wall is a function of time and adjusted every cycle
from the velocity at the previous cycle (with a loop):
v(i) = v(i-1) + gamma*dv
Gamma is given by:
gamma = (Pext - P)/Pext
with Pext the external pressure and P the actual wall pressure computed
from the force on the wall via: P = 68568.415*abs(fwall)/area (in real
units) and fwall is time-averaged over 10 steps corresponding to one
cycle.
Everything work as expected at the beginning and the pressure equilibrates
well however after ~500 cycles, the pressure starts to diverge and rapidly
becomes chaotic and the simulation crash.
I would appreciate any advice to solve this.
when you adjust the wall to the full extent in every step, you open
yourself to feedback and your plot looks like that happened to you. the
system you construct is not very different from an oscillator.
you want a damped or better and overdamped oscillator. check out the
berendsen thermostat algorithm. in short, you don't want to apply gamma,
but gamma times the damping factor, which should be of the order of 1000 to
100000 time steps.
axel.

Dear Axel,
I went over Berendsen’s paper and slightly modified my input file accordingly:
mu = 1-(timestep/tau)*(P-Pext)
v_i = v_(i-1)*mu
With tau = 10,000, I obtain reasonable equilibration of the pressure.
I attach P in Atm = f(cycle) on both walls with Pext = 1,000 Atm.
Thank you.
Nicolas