Hi,
I’ve just started using pymatgen and I’m trying to use it to retrieve a list of substructures from structures that become increasingly vacant of one type of atom. My original unit cell is quite large (40 of the atom I want to remove), and I want to get a list of several candidate substructures and not just the same one with the lowest Ewald energy. To do this I am using the PartialRemoveSpecieTransformation from pymatgen.transformations.standard_transformations.
The code is roughly something like this:
from pymatgen.transformations.standard_transformations import PartialRemoveSpecieTransformation
# load .cif-file and store in variable 'structure'
for i in range(1,number_of_atoms+1):
trans = PartialRemoveSpecieTransformation(ion_to_remove, i/number_of_atoms)
substructures = trans.apply_transformation(structure, return_ranked_list=5)
# write each substructure to a separate POSCAR
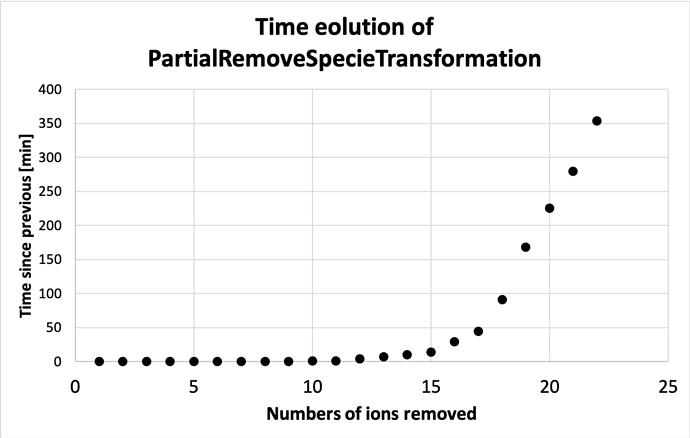
I’ve run into some scaling issues doing this. So the first 8-10 fractions goes OK, and then it starts to slow down. Not unexpected. After some hours it successfully spits out the substructures for the half-way point, but after this the time between each new set of substructures still increases.
Should not the midway point be the most demanding set to produce, with \binom {40} {20} combinations? And after this it should decrease again?
As you can see I have not explicitly set the algorithm used for this - I’m not sure which one is used by default when asking for a ranked list (as I understand the fast algorithm will only return one sbustructure?)
Hi @rasmusthog, welcome!
Can you verify the time issues you’re reporting by running an individual transformation, rather than all at once? The kind of progressive slowdown you’re mentioning sounds a lot like a memory leak.
To be able to investigate further we’d have to have the CIF file you’re trying (or one that’s similar to it).
Best,
Matt
Hi Matt, thanks!
I’m running some individual transformations now for removing 21 - 25 of the total 40 atoms now. I’ll update when they finish running.
Here’s a structure that is comparable in size: https://www.materialsproject.org/materials/mp-19511/
In the meantime, I’ve plotted the time evolution underneath.
So after having run 10 individual runs from a fraction 21/40-30/40, it seems that the run time comes down after peaking at a fraction of 23/40. The run times are not exactly the same as for the ones run in a loop with the code posted above, and actually somewhat longer (5 hrs 39 minutes vs. 4 hrs 39 minutes for 21/40 for example).
I’ve submitted a new job to do the whole thing in a for loop, and allow it to run for some days to see what I get. However, we’re nearing the end of an allocation period on the hpc-cluster I’m running my jobs, so the queues are massive at the moment. I will post the results when I have them.
At least it seems that my worry that the run time continued to increase past the midway point was not the case. Just wondering: is there a reason to expect that the fraction that will use the most computing time would be something other than 1/2?
Hi again,
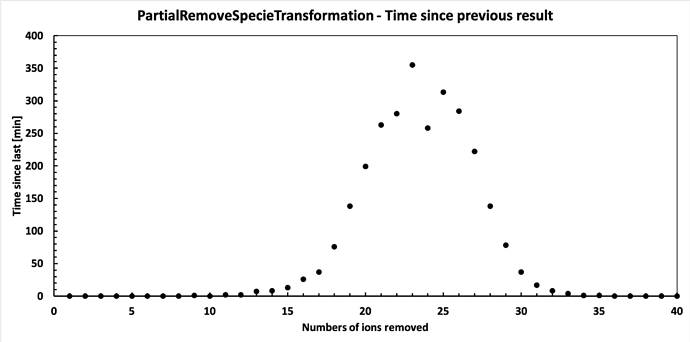
Finally it has finished running. Below are the results. Seems it follows a binomial distribution fairly nicely, but with a peak shifted from the midway point. I find this interesting, but perhaps there is an obvious reason for it?
Anyway, thanks for the help - I believe my issues are solved. My concern was that it would keep scaling, but it clearly doesn’t.
Cheers!