Dear Users,
I plan to run a polymer adsorption simulation on Silica substrate. This polymer is solvated in water. I plan to use NVT simulations with p p f periodic boundary conditions along with kspace_modify slab 3.0 option. In addition, I plan to use a reflecting wall for water molecules at the Z edges of the system so that I dont loose them.
I wanted to ask the experts who have run similar simulations before. In Z (non-periodic direction), should I keep this dimension which correspond to my applied pressure (no space between the reflecting wall and the ‘free’ surface of water) or should I 2-3 nm of vacuum on top of the free surface of water?
The water (near the free surface) will not interact with the substrate because of non-periodic nature.
I have attached a basic schematic for the two scenerios. I will appreciate if anyone has any other insightful comments.
Best Regards,
Vikas
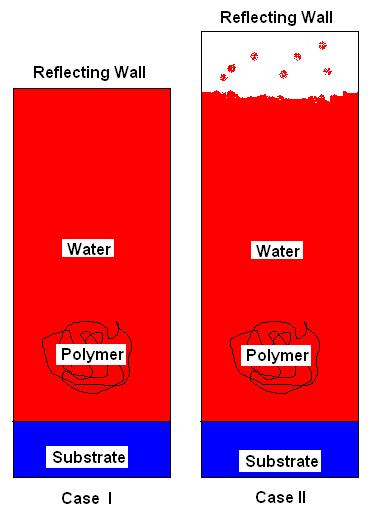
Vikas,
I have simulated similar systems before. Generally I use an LJ93 wall boundary since it gives a more structured boundary. This way, you can approximate the equilibrium gap that should exist between your water and wall. In either case, you will need to provide a small buffer between the water and wall to maintain the correct (approximate) pressure.
The structure of the water near the wall should not be too significant because it is so far-field. The effects of the wall may persist 2-3 atomic diameters into the fluid, but that looks to be sufficiently far from your polymer/substrate region.
Jonathan
Dear Dave, Jonathan,
Thanks for the responses. I will try to incorporate your suggestions for sure. Now, I have one more question. At the reflecting wall, Z component of the velocity reverses sign, wont the total momentum of the system will not be conserved and might eventually become important. Did any of you see such shifting of coordinate system, later in your simulations.
Vikas,
I’m not sure how to address this rigorously. I guess the wall is considered to have infinite mass. I tend to use the LJ walls instead of the reflecting walls, but the issue is still relevant. In my cases, I have not observed anything unusual. I’m not sure how this issue might manifest as a problem since the system is still constrained to an absolute location in space. Sorry, maybe somebody else can address this better.
Jonathan
I've had problems with the reflecting wall and energy conservation. I suggest a wall with a smooth potential, like a 12-6 or 9-3.
Matt
