Dear lammps group:
I would like to know if any one has tried to compute stress fields near crack tips.
When I tried to compute local atomic stresses using lammps compute stress/atom, I could never succeed in atleast qualititatively reproduce the stress fields as predicted from continuum mechanics. ( example the expected stress concentration near the crack tip is never acheived).
I would like to know if it is possible to generate stress fields from atomistic simulations.
Thank you
Murali
Should the atomic stress fields match continuum?
Steve
Hi Murali & Steve,
I’ve spent a good part of my professional career trying to answer this question. For the atomic stress calculated from the virial expression, one does indeed get a stress field qualitatively similar to a classic crack tip stress field. This has been shown by several authors in the literature, I suggest looking up articles by Abraham, Marder, Farkas and X. Zhou (just off the top of my head). I myself have done a few studies looking at crack tip stress fields, and a picture of one (for an MD simulation using lammps’ predecessor code ParaDyn) is attached below:
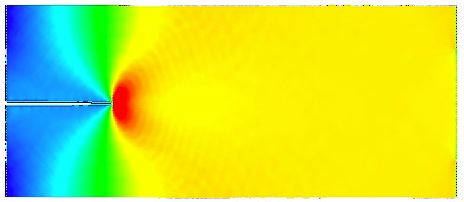
There are a few known issues with the atomic stress as compared with a continuum measure of stress. First, as one would expect the stress field is not singular as one approaches the crack tip. Rather, it reaches a finite maximum reflective of the non-local nature of the inter-atomic potential. Second, the behavior of the stress field is ill-defined near free surfaces (as noticed by Cheung & Yip and Zimmerman et al). Thus, recent publications from various authors (Hardy, Cormier et al., M. Zhou, Murdoch) have defined continuum measures of stress that can be extracted from atomistic quantities of force, position and velocity. These expressions are similar to, but differ from, the virial/atomic expression.
Jon Zimmerman
Hi, Jon, Murali & Steve,
This is an very interesting topic for mechanical pepole because they always have a speculative view that the results of continuum based theory can still be applicable to the atomic scale. This is a very nice snapshot proving that elasticity is still accurate even the length scale is very small.
What I want to mention is that the importance of the boundary condition, I guess the imposed boundary condition is the fixed displacement boundary condition according to the K field (which is used to resemble a infinite large sample under loading while the interaction of the atomistic region and the outer is applied by the boundary condition). Am I understand right? please correct me if I am wrong.
AC

Ajing,
You’re correct that boundary condition impacts the resulting stress field. For the simulation depicted I was using a fixed displacement at the top (u_y = some constant value) and bottom (u_y = 0) boundaries, and free conditions at the side boundaries. The simulation (and the lattice) is 2-dimensional, so there is no third dimension to apply bc’s for.
This is NOT the same bc as a prescribed K field. That would require a prescribed, spatially-varying displacement field along all four boundaries. However, the system is large enough such that the characteristic “peanut” shape of the normal stress field for the vertical direction still appears.
Jon Z.

On the other hand, some studies have shown that continuum mechanics seriously breaks down at the atomistic scale (e. g. Luan and Robbins, Science 2005). How badly it breaks down depends very much on the details of the problem. My two cents, it’s a complicated issue and at the very least one shouldn’t assume an MD simulation will quantitatively match an analytic continuum model, especially if the stresses are large.
Best,
Rob
