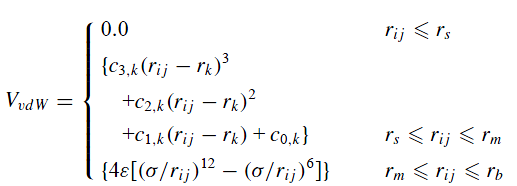Dear Steve,
Currently we are investigating friction putting diamond-like carbon tip above the amorphous carbon film.
We use the Tersoff potential for bond, while van der Waals for nonbond.
However, we need to separate van der Waals to four regions in term of cut-off
1: when r <= 2.0 angstrom, van der Waals=0
2: when 2.0 < r <= 3.4 angstrom, we use switching function (spline fit) to standard LJ
3: when 3.4 < r <= 8.0 angstrom, we use original LJ formula
4: when 8.0 < r <= 10.0 angstrom, we use lj/smooth, so that at the 8.0 angstrom inner cutoff the force match the unsmoothed LJ formula. At the 10.0 angstrom outer cutoff the force will be 0.0.
Similar to the following format
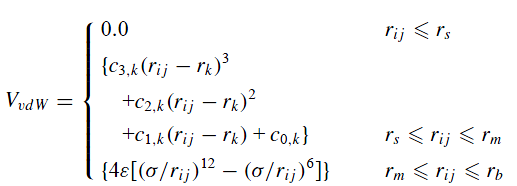
Our question is how to do this possible in lammps?
Thanks a lot and best regards
Zhendong
You have 2 choices:
a) tabulate the potential over its entire range and use pair-style table
(as part of pair_style hybrid, with the Tersoff potential)
b) code up the potential as a new pair_style foo, similar to
pair_style lj/smooth, which you could look at.
Steve
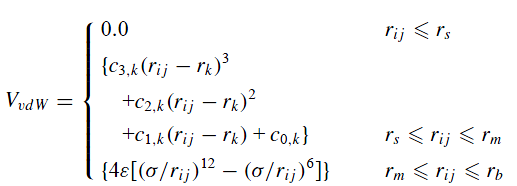
Dear Steve,
Thanks a lot!
Yes, exactly we are trying to use the pair-style table.
Best regards
Zhendong
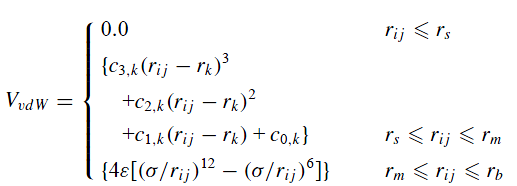
Dear Steve,
There are several potentials for SiC in LAMMPS.
But they are suitable for crystalline-SiC.
There is a good potential for both crystalline SiC and amorphous SiC( http://cacs.usc.edu/papers/Vashishta-SiCpot-JAP07.pdf )
Source: JOURNAL OF APPLIED PHYSICS 101 (103515) 2007
Title: Interaction potential for silicon carbide: A molecular dynamics study of elastic constants and vibrational density of states for crystalline and amorphous silicon carbide
Authors: Priya Vashishta, Rajiv K. Kalia, Aiichiro Nakano and José Pedro Rino
University of Southern California, Los Angeles, California 90089-0242
Is it possible to include this SiC potential in LAMMPS?
This will be wonderful for authors who use LAMMPS to investigate crystalline SiC, amorphous SiC and nanocrystalline-SiC.
Thanks
Best regards
Zhendong
Dear Sha:
The most effective way to get a new potential in LAMMPS is if a user who is motivated to use it goes ahead and implements it, and then shares it with the community. It’s an open-source code, so there’s no reason you can’t try to code it up yourself!
—AEI
That is correct. Also, this particular potential has a similar structure
to the Stilinger-Weber potential that is already implemented in LAMMPS
(pair_style sw). Hence, you could proceed by copying the pair_sw.cpp/h
files to, say, pair_vashishta.cpp/h. A smart text editor like emacs can be
used to quickly change all instances of sw and SW to vashishta, Vashishta,
and VASHISHTA, as appropriate. Once you can compile and run pair_style
vashishta (reproducng the SW potential), you can modify the relevant
function bodies to get the new potential. All of that should take about a
day. What may take more time is verifying that all the parameter values
are specified in the correct units, etc, so as to reproduce the results in
the paper. For that, it is always nice to have the original code to
compare against.
Aidan