Hi,
I met a problem in benchmarking the LJ force for a very simple system, and the problem is the force profile does not have the same symmetry as the system. The input files as well as output are attached.
The system is one atom interacting with a chain of atoms (see sys.gro for configuration) through lj/cut. The atom is moved along the chain at a constant velocity, so in the end what you get is a force profile along the axis f(x).
As the chain is with fixed lattice constant, the profile should be symmetry, however, it turns out that this is not the case.
I have used a large cutoff and updated the neighbour list every step. While the cut method would increase some discontinuity, I don’t think it will affect a symmetry as with in one lattice I have ~600 evenly distributed points.
So, could anyone help me solve this. This problem seems simply, but it worries me as I used it as a benchmark…
Best
Ming
lj.tar.gz (108 KB)
Hi,
I met a problem in benchmarking the LJ force for a very simple system, and
the problem is the force profile does not have the same symmetry as the
system. The input files as well as output are attached.
The system is one atom interacting with a chain of atoms (see sys.gro for
configuration) through lj/cut. The atom is moved along the chain at a
constant velocity, so in the end what you get is a force profile along the
axis f(x).
As the chain is with fixed lattice constant, the profile should be
symmetry, however, it turns out that this is not the case.
it has the symmetry that it should have. it is fairly straightforward to
explain this with simple geometric considerations.
axel.
I have used a large cutoff and updated the neighbour list every step.
Hi Axel,
Thanks for your reply. However I don’t understand from which point you think it has the symmetry. For your convenience, here I attached the results as figures, which is another of presenting the results I sent before.
Fig (a) is the system, a particle moving along a 1-D crystal at a constant velocity at zero K. The atoms in the chain are fixed. Fig (b) is the force exerted on the particle by the substrate along the axis.Obviously from Fig. a we know that every cycle, the force should be symmetric, that this is not the case calculated by LAMMPS. As I stated before, the systems is simple and I’ve paid attention to technical details. So I’m afraid does this ‘benchmark’ show that this is some errors in the force calculation of LAMMPS?
Best
Ming
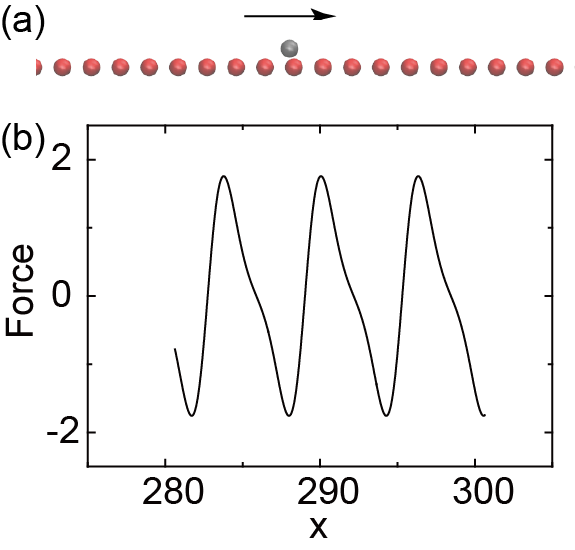
Hi Axel,
Thanks for your reply. However I don't understand from which point you
think it has the symmetry. For your convenience, here I attached the
results as figures, which is another of presenting the results I sent
before.
Fig (a) is the system, a particle moving along a 1-D crystal at a
constant velocity at zero K. The atoms in the chain are fixed. Fig (b) is
the force exerted on the particle by the substrate along the axis.Obviously
from Fig. a we know that every cycle, the force should be symmetric, that
this is not the case calculated by LAMMPS. As I stated before, the systems
is simple and I've paid attention to technical details. So I'm afraid does
this 'benchmark' show that this is some errors in the force calculation of
LAMMPS?
there is no error in LAMMPS and - as i said before - the graph looks the
way it should be. it *does* have the right symmetry in the right places. it
can be easily explained from a few simple geometric considerations. just
saying "it must be 'symmetric'" is no argument. i'll give you one more
hint: remember that you are looking at the force in the direction of the
motion of the particle, not orthogonal to it.
axel.
Hi Axel,
This is a good puzzle… I just plot the force orthogonal to it, and it is symmetric, just as what you said. But I still don’ understand while the force along the axis is not symmetric. I’ve also asked the same question to my friend here just then and he thought it should be symmetric too. So, could you please kindly explain me the reasons… I’ve been puzzling by this for two days… Thanks a lot!
Best
Ming
Hi Axel,
This is a good puzzle... I just plot the force orthogonal to it, and it is
symmetric, just as what you said. But I still don' understand while the
force along the axis is not symmetric. I've also asked the same question to
my friend here just then and he thought it should be symmetric too. So,
could you please kindly explain me the reasons.... I've been puzzling by
this for two days.... Thanks a lot!
let me repeat. the graph *is* symmetric. you have two points of inversion
symmetry per period and that is exactly what should be there. if this would
be incorrect, LAMMPS would be incorrect at such a fundamental level that
people would have long ago noted it, considering how much this feature is
used.
as for the explanation, please keep in mind that when you are looking at
the x-component of the force, it passes *twice* through zero, once when you
are exactly at the same x value as an atom of your line of atoms and once
when you are in the middle between two atoms. at each of these points the
sign of the force has to change. that is because you are repelled by an
atom in front of you or behind you or you are attracted more by the
previous atom you passed or the next atom. since the repulsive branch of a
LJ potential is steeper than the attractive, these two cannot be of the
same magnitude which explains the different shapes. yet it also explains
that graph is symmetric (same magnitude, opposite sign) around the points
where it goes through zero.
as simple as that. tell your friend, too.
axel.
p.s.: there is a lesson here: don't ever trust your intuition, when you can
argue with geometry. break down the problem into something simpler. in this
case, it all comes down to simple function analysis. only that you don't
know the exact function here, since it is a superposition of many) but you
know some properties that it has to have. and that is straightforward
high-school level math. 
Hi Axel,
Many thanks!!! With your detailed explanation, now I understand. Yes, as you said, this is really a good lesson for me 
Best
Ming


