Dear MD society,
I have a question regarding the calculation of embedding energy of the EAM (Embedded Atom Method potential) potential type. In the paper of “Phase stability in the Fe-Ni system: Investigation by first-principles calculations and atomistic simulations (as attached)”, it is stated that the embedding energy is calculated by inverting the universal equation of state (shown as in the picture below, E(a) is the crystal energy per atom relative to a set of isolated atoms, E0 is the equilibrium cohesive energy (minimum energy of E(a)), a is the cubic lattice parameter, a0 is the equilibrium value of a, Omega0 is the equilibrium atomic volume, B is the bulk modulus, and beta is just a parameter). I have three questions regarding this calculation:
(1) This universal equation of state (equation 9 as shown below) is independent of electron density, but an equation of cubic lattice constant a, while the embedding energy F should be an equation of electron density (\rho). Then how the equation 9 relates to the electron density?
(2) How the equilibrium atomic volume Omega0 is calculated? Using 4/3pir^3 (r is the atomic radius = sqrt(2)a/4 in fcc lattice), or a0^3/4 (a0 is the equilibrium value of a in equation 9, this is from the paper: Atomistic modeling of the γ and γ’-phases of the Ni–Al system)?
(3) What does the “inverting” mean here? The embedding energy = 1 / EOS (equation of state)?
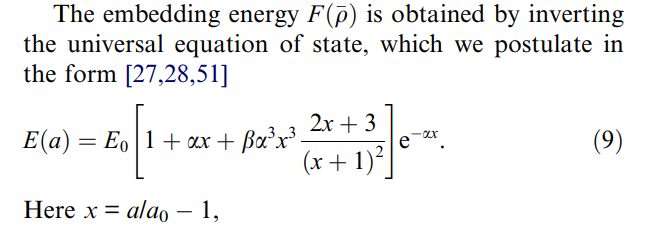
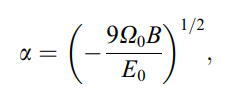
Really appreciate if anyone can provide some information here! Thanks a lot!
Best,
Jiaqi
EAM_Ni potential.pdf (332 KB)