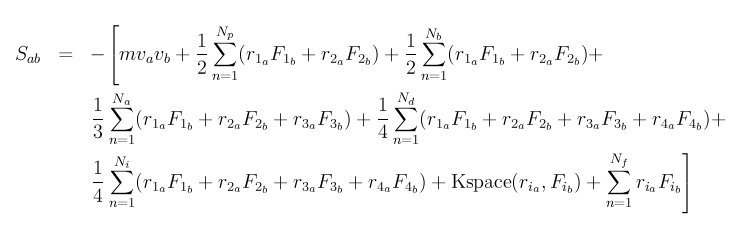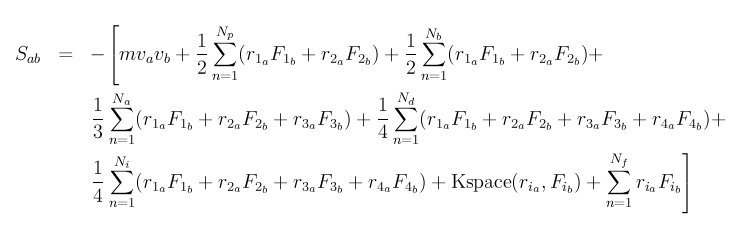stress per atom calculation

LAMMPS LAMMPS Mailing List Mirror
1

Dear Diaz,
Thank you very much for your help. Actually, You have exactly mentioned to what I have confusing about. if we use Fij*rij which is virial pressure

Stress X (i)= -(m* Vx(i)* Vx(i) + Sum ( Fijrij )) where rij= ri-rj ??? OR Stress X (i)= -(m Vx(i)* Vx(i) + Sum ( rx(i)*Fij+rx(j)*Fij)) ???

Sincerely,

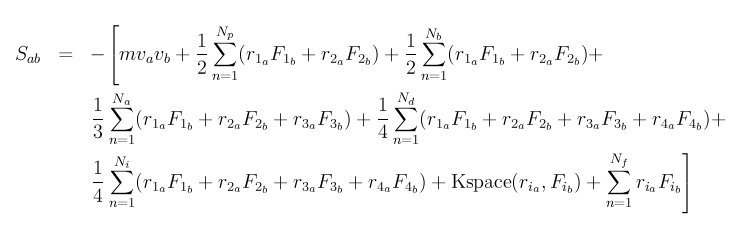
image.png

2

Greetings,

That mathematical equation can be figured out by multiplying out Fijrij= Fijri-Fijrj=Fijri+Fji*rj. Summing over all j and i and acknowledging that sum(Fij)=Fi for j not equal to i gives the resulting Stress in terms of total particle force and particle position.

Sincerely,

Adrian

image.png

3

Got it. thank you very much for your clarification. I was really confused.

image.png

4

Hi,

I would like to add something on this topic.

For two-body potentials, per atom virial tensor on atom i, W_i, is:

W_i = r_i \otimes F_i (this is a definition and here r_i and F_i are vectors)

Using periodic boundary conditions, it can be transformed to:

W_i = 1/2 * \sum_{j != i} r_ij \otimes F_ij

Here, r_ij = r_i - r_j is the relative position vector, and F_ij is the force vector acting on i due to j.

For many-body potentials, the LAMMPS implementation generalizes these formulas in some way, although I don’t think it is rigorous.

Bruce

image.png

5

Dear Adrin,

Therefore, the difference between stresses in X and for example y direction is only because of the kinetic part of the equation. tight? the energy or virial part is the same in all stress tensors.

Sincerely,

image.png

6

Dear ALL,

Thank you very much for sharing your ideas. I finally found out what is happening. but believe me the formula has been explained very complicated.
Sxx (i) = -( mVx(i) Vx(i) +0.5* SUM over bin ( Fij . ( rx(i) - rx(i) ))
Syy (i) = -( mVy(i) Vy(i) +0.5* SUM over bin ( Fij . ( ry(i) - ry(i) ))

and so one…

Sincerely,

image.png

7

Your formulas are still incorrect. The explicit per-atom stress tensor for
(short-ranged) two-body potentials can be written as:

Sxx_i = m_i vx_i * vx_i + 0.5 * sum_j Fx_ij * (x_i - x_j)

Sxy_i = m_i vx_i * vy_i + 0.5 * sum_j Fx_ij * (y_i - y_j)

Sxz_i = m_i vx_i * vz_i + 0.5 * sum_j Fx_ij * (z_i - z_j)

Syx_i = m_i vy_i * vx_i + 0.5 * sum_j Fy_ij * (x_i - x_j)

…

Best,
Bruce

image.png