Dear LAMMPS users and developers,
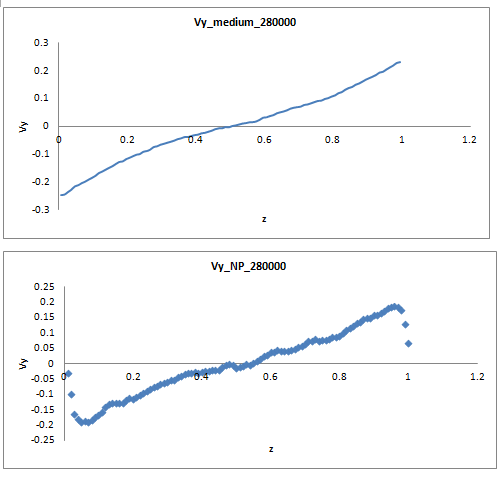
I have been stuck with linear velocity problem for a sheared system for a long time, and I attached so far the best results of the velocity profile that i am able to obtain. I wonder if you can let me know if it is still faulty or it is acceptable.
My system is composed of rigid bodies as NP, while medium is just simple solvent.
The command I am using to apply shear is:
fix shear medium deform 1 yz erate 0.01 remap v
compute stream medium temp/deform
The command that I am using to output the spacial configuration is:
fix o1 medium ave/spatial 1 10000 10000 z lower 0.01 vx vy vz density/number ave running units reduced file s001_med.medium.space
fix o2 NP ave/spatial 1 10000 10000 z lower 0.01 vx vy vz density/number ave running units reduced file s001_med.NP.space
fix o3 all ave/spatial 1 10000 10000 z lower 0.01 vx vy vz density/number ave running units reduced file s001_med.all.space
The plots shown here are after a very long time shear already. The standard deviation in number density of NP is 0.008. I am expecting to see perfect linear profile without curvature in the middle and without kinks nearby boundaries.
Please share your opinions with me. I appreciate it.
Regards,
Ling
Li,
How are you time integrating your system? Have you tried using “fix nvt/sllod” ?
Carlos

Ling,
Some time ago I found a possible bug in the fix_ave_spatial.cpp but I did not have time to do a proper test. Before trying to change any code, could you change your simulation to use another axis instead of z?
The related lines in fix_ave_spatial.cpp are:
1185,1186c1185,1186
< if (zremap < boxlo[kdim]) zremap += prd[kdim];
< if (zremap >= boxhi[kdim]) zremap -= prd[kdim];

yes - this was a typo bug which could affect the bins atoms are in that go outside
the domain in the z direction if the system is periodic in z
Will be fixed in the next patch. Please tell us if the change fixes
your profile problem.
Thanks for catching this,
Steve

Thanks all!
Mario and Steve, so the problem here is with applying shear on y direction and vorticity in z direction? I will change the shear direction to see what’s happening.
Regards,
Ling

Hi all again,
I actually sheared the system without NP,pure solvent. I output spatial configuration on z direction, and I was able to get linear profile after very long time shear. So I wonder if actually the main problem here is with the rigid bodies? To put it more specifically, the rigid body get straddled across the z-boundary, and that explains why in the velocity profile of NP, we see kinks nearby the boundary? What do you see?
I attached here the velocity profile of a pure solvent system, y is the shear direction while z is the gradient direction. Different lines stand for output interval.
Output command for this sheared system is:
fix shear all deform 1 yz erate 0.002 remap v
compute stream all temp/deform
fix o2 all ave/spatial 1 10000 10000 z lower 0.01 vx vy vz density/number ave running units reduced file all_s0002.space
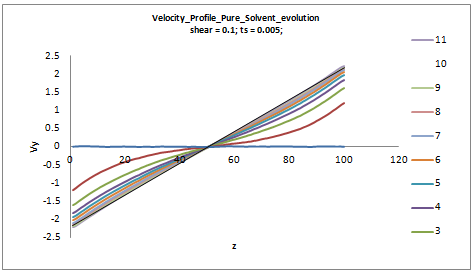
But anyway, I will change the shear and gradient direction to see the change.
Thanks again!
Ling

The easiest thing for you to try is to apply the bug fix that Mario sent,
either directly from his email or download yesterday’s version of
LAMMPS which has the patch. That may help the NP case.
For non-NP (pure solvent), if you are doing “remap v”, it shouldn’t
take that long for the system to come to equilibrium with the
box deformation rate.
With NP, I think they should also come to equilibrium with
the solvent flow and thus the box deformation rate. However,
NP that straddle the shearing boundary may be problematic
for how their sub-particle velocities are binned. I think their
dynamics should be correct as an NP crosses that boundary.
However, the individual sub-particles have to have the
shear velocity added/subtracted as they cross the boundary.
As I recall, that happens when the center-of-mass of the NP
crosses. However fix ave/spatial knows nothing about the NPs
and may use the periodic boundary to bin a sub-particle
in a bin on the other side of the box, when its velocity has
not yet been remapped. If I’m correct, the effect would be
to perturb the values in bins up to 1/2 the diameter of the NPs
on either side of the boundary.
Steve



