Hi all,
I have followed the below link for the task.
After updating the force_constants.py, it didn’t give the correct fc4.hdf5 file. So, I modified it accordingly to get the fc4.hdf5.
def write_to_phono3py(self, fname: str, order: int) -> None:
"""
Writes force constants in phono3py format.
Parameters
----------
fname
name of file to which to write third-order force constant
order : int
order(3+)
"""
if order == 3:
phonopyIO.write_phonopy_fc3(fname, self)
elif order == 4:
phonopyIO.write_phonopy_fc4(fname, self)
else:
raise ValueError('invalid order! only up to 4th order is accepted')
#phonopyIO.write_phonopy_fc3(fname, self)
However, I am still getting the below error. Is it a memory issue or something else because I am using a machine with 32 GB RAM with 16 cores?
fcs.write_to_phono3py('fc4.hdf5', 4)
File “/home/ashis/miniconda3/envs/1my_env/lib/python3.8/site-packages/hiphive/force_constants.py”, line 471, in write_to_phono3py
phonopyIO.write_phonopy_fc4(fname, self)
File “/home/ashis/miniconda3/envs/1my_env/lib/python3.8/site-packages/hiphive/input_output/phonopy.py”, line 188, in write_phonopy_fc4
fc4_array = fc4.get_fc_array(order=4)
File “/home/ashis/miniconda3/envs/1my_env/lib/python3.8/site-packages/hiphive/force_constants.py”, line 121, in get_fc_array
fc_array = np.zeros((self.n_atoms, ) * order + (3, ) * order)
numpy.core._exceptions.MemoryError: Unable to allocate 162. GiB for an array with shape (128, 128, 128, 128, 3, 3, 3, 3) and data type float64
Best regards,
Ashis
Yes dense force constants can become very large. You could try to modify line 121 to use a sparse format if you want. You can also check the get_fc_dict method of the ForceConstants object.
Hi Fredrik/Erik
I compared the 4th-order Interatomic Force Constants (IFCs) calculated using hiphive and fourthdorder.py (FourPhonon). I observed a substantial discrepancy when visualizing the relationship between the IFC norms and perimeters. However, for 3rd-order IFCs, the deviation is relatively minor. I have generated 300 MC_rattle structures for the calculations. I have used 6th-order cutoff for the generation of fcp.
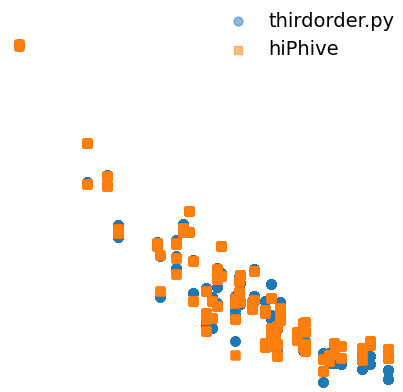
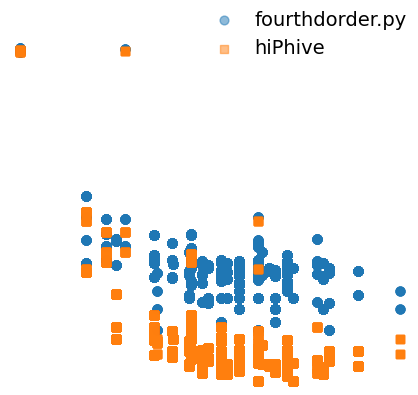
I have used the following lines to generate the structures (I have two atoms in the unit cell)
n_structures = 300
cell_size = 5
dim = 5
rattle_std = 0.03
minimum_distance = 2.10
prim = read(‘POSCAR’)
#atoms_ideal = prim.repeat(cell_size)
atoms_phonopy = PhonopyAtoms(symbols=prim.get_chemical_symbols(),
scaled_positions=prim.get_scaled_positions(),
cell=prim.cell)
phonopy = Phonopy(atoms_phonopy, supercell_matrix=dim*np.eye(3),
primitive_matrix=None)
supercell = phonopy.get_supercell()
supercell = Atoms(cell=supercell.cell, numbers=supercell.numbers, pbc=True,
scaled_positions=supercell.get_scaled_positions())
print(prim)
structures = generate_mc_rattled_structures(supercell, n_structures, rattle_std, minimum_distance)
write(‘prim.extxyz’, prim)
write(‘supercell_ideal.extxyz’, supercell)
write(‘supercells_rattled.extxyz’, structures)
What are the factors that can improve the discrepancy of the 4th-order IFCs? How important is the choice of rattle_std and minimum_distance value?
Best regards,
Ashis
What are you plotting on x and y axis, is it a log-scale? I guess its the norm of fcs vs radius of the cluster?
It looks like the large fourth-order FCs are the same with either method.
In principal the FCs should decay to zero for long interatomic distances.
In your plot it looks like they decay and then reach some plateau value (probably related to limited accuracy of the methods to resolve 4th order FCs?), and this plateau value is different between the two methods?
This is what I have plotted
Anharmonic IFC norm vs quadrilateral Perimeter
I think the large fourth-order FCs do not look similar.
Try to establish your noise level. As Erik said It looks like the difference you see is just due to noise. There are many aspect to take into consideration when comparing force constants from different methods.
- How well posed is you fit problem? Do you have enough data to fit up to 6th order?
- What is the effective temperature of your input data? Are you sampling an effective potential?
- How did your convergence study look like for the fourthorder and for hiphive with respect to displacement parameters?
- How do the two force constants compare when cross predicting data?
- Which regularization did you use? Does it change the fit if you change the hyperparameter?
- The mc rattle method takes a keyword n_iter which is related to the final effective displacement as sqrt(n_iter) * rattle_std which for some reason is not mentioned in the docs @erikfransson ?
Try around with these suggestions. Try to compare the thermal conductivity with both force constants and see if there is any difference.
How well posed is you fit problem? Do you have enough data to fit up to 6th order?
=> I don’t know how much data I need to fit up to the 6th order. Can you please comment on it?
I also tried to fit up to 4th order, but the results are more or less similar. In the beginning, I compared the thermal conductivity with 3rd-order ph-ph interactions only, and I found an excellent match between the hiphive and shengbte result. The mismatch appears when considering 4th-order ph-ph interactions.
===================== Optimizer ======================
seed : 42
fit_method : least-squares
standardize : True
n_target_values : 151500
n_parameters : 3254
n_nonzero_parameters : 3254
parameters_norm : 16.6868
target_values_std : 0.7584998
rmse_train : 0.02432366
rmse_test : 0.02483946
R2_train : 0.9989735
R2_test : 0.9989094
AIC : -1006929
BIC : -974964.6
train_size : 136350
test_size : 15150
======================================================
What is the effective temperature of your input data? Are you sampling an effective potential?
=> I didn’t consider the temperature effect yet. I have MC-rattle to generate the structure.
How did your convergence study look like for the fourthorder and for hiphive with respect to displacement parameters?
=> I also suspected this thing. The displacement parameters can improve the mismatch. I have tried different displacements in fourthorder and got more consistent results with hiphive. However, the final comment can be made after a detailed thermal conductivity calculation.
How do the two force constants compare when cross predicting data?
Which regularization did you use? Does it change the fit if you change the hyperparameter?
=> I haven’t explored it.
The mc rattle method takes a keyword n_iter which is related to the final effective displacement as sqrt(n_iter) * rattle_std which for some reason is not mentioned in the docs @erikfransson ?
=> I have used the default one (n_iter = 10). What is the optimum value?
The number of datapoints you need depend a bit on how large your primitive cell is but you have a lot of target data compared to parameters so it is probably fine. Furthermore your test rmse is almost the same as your train rmse so there is probably no overfitting.
So it’s the LTC that differs a lot and not only the size of the 4th-order force constants? In that case I would compare the rmse after removal of the predicted forces that comes from second and third order elements.
The mc rattle method with n=10 and std=0.03 will produce effective displacments of roughly std=0.1. This might be to large for you application but then again your fits look decent. There is no optimal value but is system dependent.
As I mentioned I would check how well the force constants from fourthorder.py predicts the forces in the mc-rattled structures and vice versa, using the force constants from hiphive and predict the forces from the fourthorder.py dataset.
From your plots it look like fourthorder.py contains more noise since the norm of the force constants are higher and independent of distance. Try to fit the force constants in series (first second order and then third order on residues and finally fourth order on the final residues from third order fit).
Fitting higher orders are hard since the displacement must be large enough to discern the anharmonic effects from noise in the target (DFT) data. My preferred way is to generate displacements from phonon-rattle using the 0K harmonic force constants or effective harmonic force constants via e.g. mc-rattle bootstrap. I would then fit all orders in series.
In addition to the above recommendations (especially cross checking the force constants) I would first fit second and third order and use them to remove those contributions from the target data. Then I’d use e.g. ARDR, ridge or some post-LASSO technique as illustrated in Eriks paper and run a hyper-parameter scan for only the fourth order force constants to find out what is noise and what is real data.
Hope this helps. This is tricky business.
Hi Ashis, did you get correct 4th order force constants?

