Dear professor
Recently,I’ve been studying some of the properties of bilayer graphene using the ILP potential.
The scripts and examples provided (in lammps/examples/user/misc/ilp_graphene_hbn) are good guides
for me. But, in NVE, I find that the ILP potential seems to work well only for periodic atomic models (e.g.,
AA stacking and AB stacking), otherwise the total energy and the temperature will always goes up(Fig. 1).
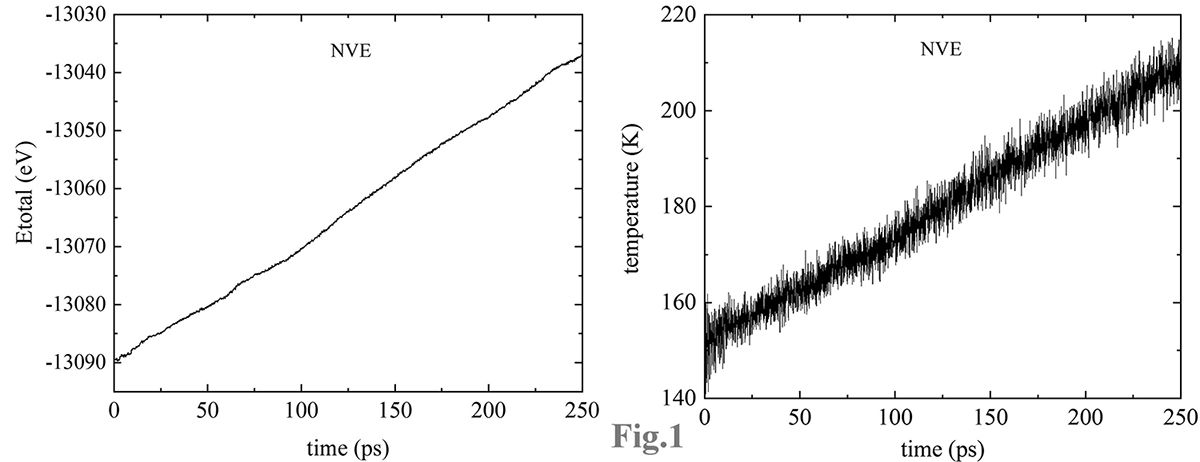
In other words, if the system being studied is of finite size with fixed boundary conditions. the etotal and
temperature will increase gradually with time in NVE. Although the rise rate is very slow, its impact on the system
will be negligible after hundreds of picoseconds (ps).
This is not an accidental case. Besides, in many simulations, the atomic models one need to build are not
periodic. For example, if I want to study the thermal conductivity of twisted bilayer graphene, Obviously,
(i) the edge of twisted bilayer is not smooth and (ii) the required simulation time is up to 1ns in NVE.
(i) indicates that the periodic boundary conditions is useless here and I need adopt the fixed boundary conditions;
(ii) means that there will be a significant increase in the total energy and temperature, leading to inaccurate results.