Dear all,
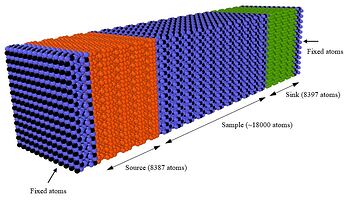
I’m trying to calculate the thermal conductivity of TiO2 using NEMD (via fix langevin). In my simulation domain, I have a Source, Sink, Sample, and the fixed atom regions as shown below. Using LAMMPS 29 Sep 2021 - Update 3.
I’m controlling the Source and Sink temperatures using two langevin fixes to 350K and 250K respectively. Number of atoms in the two regions are almost the same. However, the cumulative energy given from the two fixes to hold the two temperatures are significantly off from one another (having about 1000Kcal/mol difference, see the figure below) questioning where that excess energy went. I checked the energy conservation of the system and it is conserved. Time intergrating the atoms in the Source, Sample, and the Sink regions only. Therefore atoms in the Fixed atom regons cannot exchange energy with the Source/Sink. Any comment on the issue is highly appreciated.
Thank you, Best regards.
Chamara.
1 Like
The problem is your overall setup. Typically, these kind of simulations use a periodic “sample”-“hot”-“sample”-“cold”- type of setup and thus monitor the heat flux in either direction and avoid any boundary induced issues. The problem with your “fixed” zones is that those have atoms a 0K. What happens to “warm” atoms that are next to atoms that are (very) cold?
Dear Axel,
Thak you verymuch for the reply. I skipped periodic approach to save the computational time. I’m not time integrating the atoms in those two fixed atom regions and therefore, they cannot exchange energy from the hot or cold regions. I’m defining nve fix only to the Source, Sample, and the Sink region atoms (Edited the original post). So I think the problem is not from there.
Thank you
Which means you would have to run your simulation at least twice as long to get the same statistical convergence. Not sure if that is really saving you time: with a periodic setup, the hot/cold regions are used twice so you have effectively only half of them and the interactions with the immobile atoms are not needed at all.
Thank you very much Axel. I’ll look into the periodic approach.