Hi,
Perhaps you forgot to send to the mailing list.
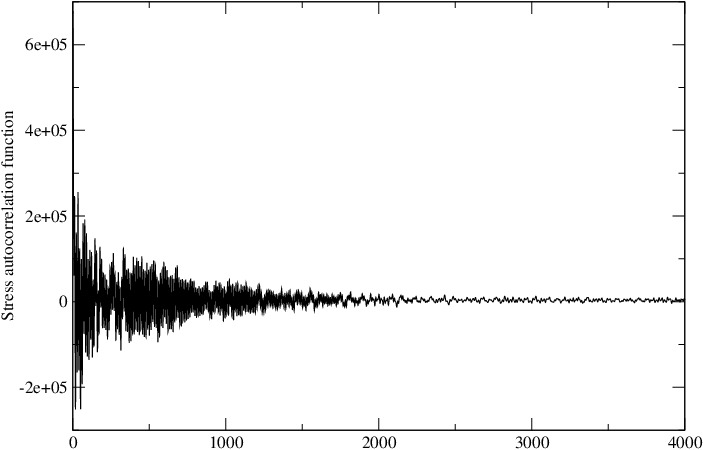
If your relaxation time is the parameter characterizing how fast the stress autocorrelation function S(t) decays, you can simply normalize it as S(t)/S(0) and calculate the time integral. Suppose S(t)/S(0) decays as exp(-t/tau), the integral is simply tau, which is a good indicator of the relaxation time.
As for your question regarding the “snapshots”, I am not clear about it. With such long simulation, you should get a very accurate time correlation function because you have about 10^7 time origins for ensemble average. [But your choice of d=ps is not good; I would use d=ps*10.]
With these parameters:
p equal 4000 # correlation length
s equal 1 # sample interval
d equal $p*$s # dump interval
You will have 10^7/4000=2500 correlation functions. Do you use “ave one” or “ave running”? I hope you are using the averaged correlation function, not just one of the 2500 correlation functions.
Best,
Bruce