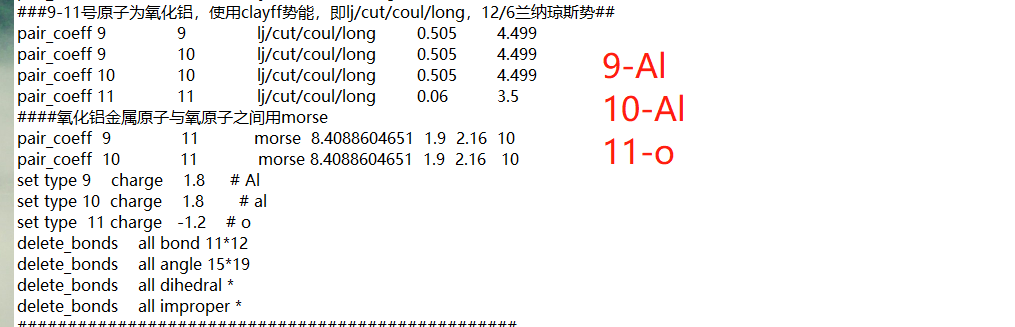
My simulation system is alumina and polyester. According to a paper, al-Al and O-O in alumina use LJ potential and Al-O use Morse potential.

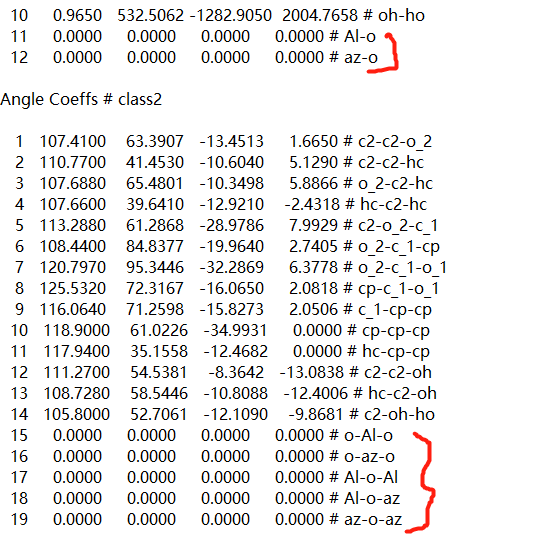
I have written the in file, but the calculation is always wrong. All angle coeffs are not set.Because data is exported by ms, the bond and angle parameters for Al2O3 are 0. I didn’t add parameters either. I don’t know if there’s a problem with writing like this.
Can you tell me there is something wrong with my program?
thank you !
10.15PCffdynmic.data (1.1 MB)
in.Al2O3-PET.lastfram (10.2 KB)
Having force constants and potential parameters set to zero is rarely a good thing unless it is done intentional. It looks like you use the ‘-ignore’ flag with running “msi2lmp” to create the data file. That will result in all parameters that are missing in your .frc file will be set to zero and you will have to add them manually by editing the data file with a text editor.
The Error message “All angle coeffs are not set”, however, has nothing to do with that. This error means, that you have more angle types than you have set parameters. This can be easily debugged by adding the info coeffs command before the first run or minimize.
It shows that the coeff data for all angles is incomplete. A closer look at the data file reveals that it is missing the required BondAngle Coeffs and BondBond Coeffs sections. Similar deficiencies seem to be present for dihedrals and impropers.
Thank you very much for your answer.
I added the info coeffs command. The display Angle is not set, but I have set it in the data file.
Looking forward to your reply.
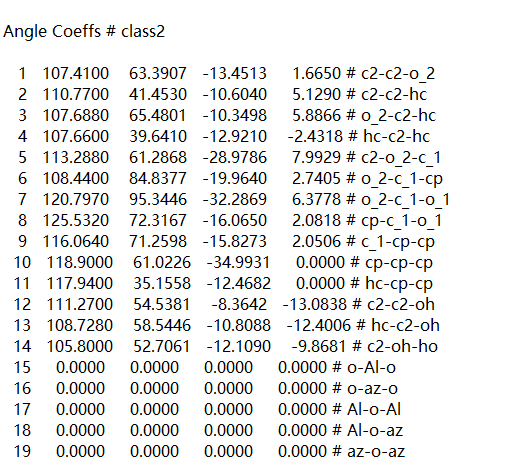
Please read my entire reply. I have already addressed this point.
The potential function for alumina is Morse. Don’t it need the parameters of its bond Angle? Then I deleted the Angle about alumina in the in file. But it goes wrong.

Your angle style is set to class2 and that requires the additional sections in the data file. The number of entries in those sections corresponds to the provided number of angle types regardless of whether you use them in the Angles section or not.
Overall this looks like you have too little knowledge about force fields and setting up MD simulations in general. I cannot provide all the explanations and tutoring you seem to be needing via a forum. You would need in person guidance for that and thus should look for someone local to assist you.
Thank you very much for your explanation