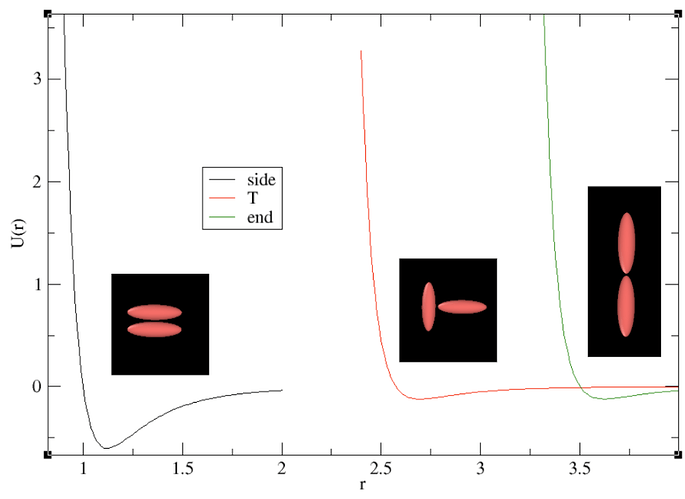
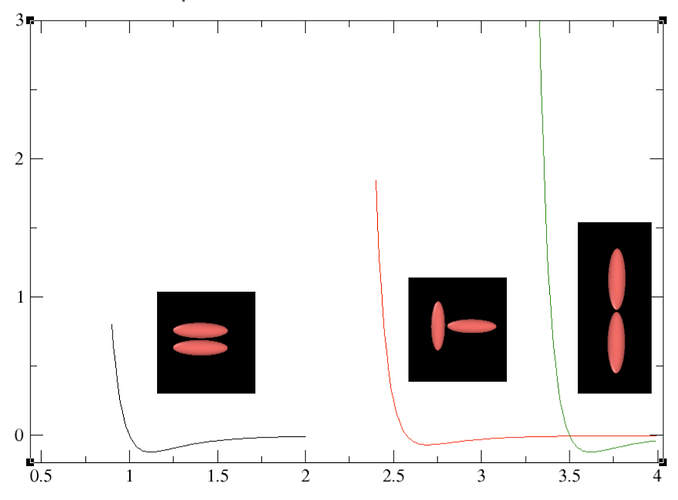
Hello,
I have a question about the gayberne potential and the ambiguity in the angles from quaternions, and different epsilon parameters. Essentially, to define any 2d it is generally recommended to use quaternions in the format:
q_0 0 0 q_3
.This define rotations around the z axis which makes sense to me. I’m simulating ellipsoids with aspect ratio 3.5, and I found literature about the potential that said that it usually safe to use the gayberne potential with the epsilon values as these:
pair_coeff 1 1 1 1 1.0 0.2 0.2 1.0 0.2 0.2
My first question is just about these because I don’t think I ever really got a good intuition about them. I know that they describe the face to face, side to side, and end to end interaction strengths but when I try to test the potential as a function of distance for different configurations I can’t really match these parameters to what I’d expect them to be based off the descriptions. I get good results with these parameters that match the typical gayberne behavior so I’m fine using them, but would like a more fundamental understanding of them. (Here is what I get using them for different configurations)
The second part of my question rises from the ambiguity in the quaternion definition of the rotation angle. For example you can describe the same angle in 2 ways (assuming you’re original orientation that you’re rotating from is 0,1,0 which I believe is mine since my ellipsoids are defined as having shape (1,3.5,1) and starting from (0,1,0) orientation), and I’ve checked this in Ovito that these produce 2 identical particles (or identical to any thing the eye can check):
1 1 3.5 1 0.02673497752 0 0 0.9996425566
2 1 3.5 1 0.568477 0.0218931 0.822265 -0.0153452
This is verified by calculating that the theta and phi angle match, using the rotation matrix from quaternions, and the rotation matrix applied to (0,1,0), which again Ovito shows me what I expect using these calculations. The problem is if I replace my 2d particles with identical versions as above using all 4 quaternions and ensuring 2d by matching
q0q1 - q2q3 = 0
q1 != 0
q2 != 0
Then I get a different potential energy curve for the same systems (the side to side no longer has a stronger well depth, but the depth locations do not change)
However when I then switch the epsilon parameters to
pair_coeff 1 1 1 1 0.2 0.2 1.0 0.2 0.2 1.0
Then I get a match to the 2d case with zeroed middle quaternions for these 3 configurations. Even then it doesn’t match the 2d for more random configurations, but its at least more similar. This doesn’t make sense to me though because the only thing thats changed is the quaternions but not the actual angle defined by them (besides maybe up to some numerical noise that’s beyond 10^-5 in angles).
I was wondering if there’s fundamentally something different about the potential with these 2 ways of defining 2d systems, or if I’m just making some dumb mistakes, or if there’s something I’m fundamentally not understanding about the different epsilon parameters? I can’t see anything obvious from the definition of the potential, or any papers I’ve found, or the lammps documentation (for example defining the epsilons as follows, but didn’t have much better luck)
I know for 2d, I should just use the q1=q2=0 case, the only reason I ask is because I’m interested in studying quasi 2d systems with small out of plane rotations where all the quaternions must be non zero.
If anyone has any knowledge on this or could even point me in specific places I might have missed I would deeply appreciate it. I’ve spent a lot of time looking into this and doing tests with the potential as a function of distance for different configurations and going through papers but I think I’m just missing some piece of the puzzle.
Thanks!