I have been struggling with the RIGID package for the past few days. My goal is to simulate two 7-particle hexagons interacting with each other. Then I need to use the trajectories to train a deep learning model. Nevertheless, I found some weird inconsistencies in the output for angular momentum and velocities.
Firstly, the angular velocity is given in system coordinates, whilst the angular momentum is given in the body coordinates (principle axes of the diagonalized inertia matrix). This could be made more clear in the docs - compute rigid/local command — LAMMPS documentation
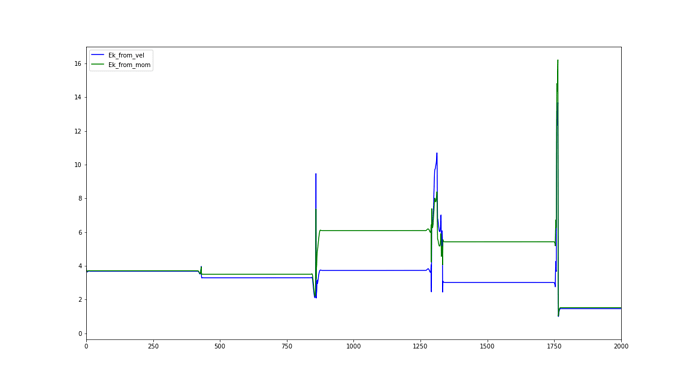
This wouldn’t be an issue, but then I found an energy/rotation inconsistency in the way principal axes seem to be defined. In other words, the angular momenta vs. angular velocities give me different rotational kinetic energies (as shown in the first plot). I take the system-fixed angular velocity, translate it into body-fixed and then calculate the energy based on the diagonalized inertia.This does not, however, agree with just taking the body-fixed angular momenta given by LAMMPS.
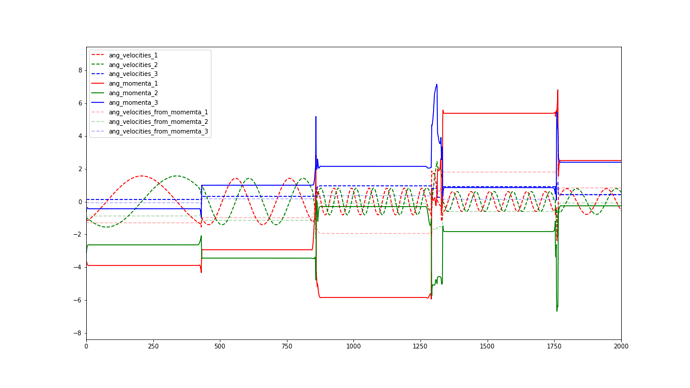
I believe this has got to do with some residue rotation, or I am not sure. If I take the angular velocity (in the system coordinates) and rotate it using the quaternion into the body axes I don’t get a ‘constant’ body-fixed angular velocity, but rather one component is fixed and the other two oscillate (that’s in the second plot - the dashed blue line is constant, but the red and green oscillate although I would expect them to be constant as there is no external torque).
(in the plots, the sharp edges are the points, when the two hexagons collide, whilst for the other regions they mostly do not interact)
I would upload my input files, but the forum does not allow that for new users so at least here - https://easyupload.io/m/fpdeha
In terms of my question, am I thinking fundamentally wrong about some part of the physics here? Or is there something else going on in LAMMPS that I am missing? I went through most of the relevant RIGID source code but couldn’t seem to find anything.