I have a problem of interpreting the autocorrelation. I made two calculations of the same problem. One at a time step of 5e-4 fms and one at 5e-5 (electron units). In both the energy was reasonably conserved.
The AC was calculated by the direct and Fourier algorithms from the book of A&T (the dump file was disentangled in per particle files with a program of Alex K. and an average over 20 - 30 particles was done). It was also calculated with a more complex program from F&S for which no disentanglement is necessary and the average is automatically included.
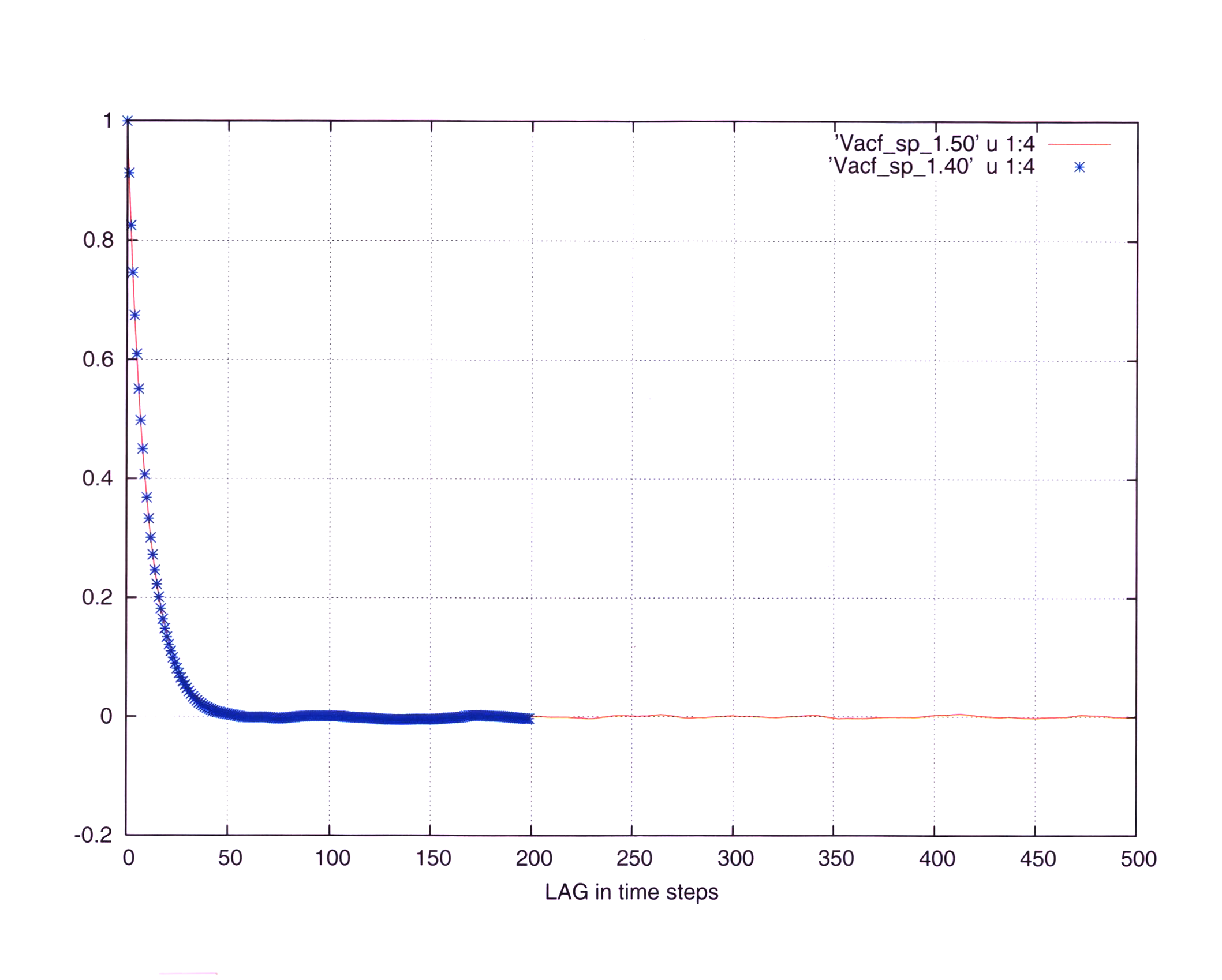
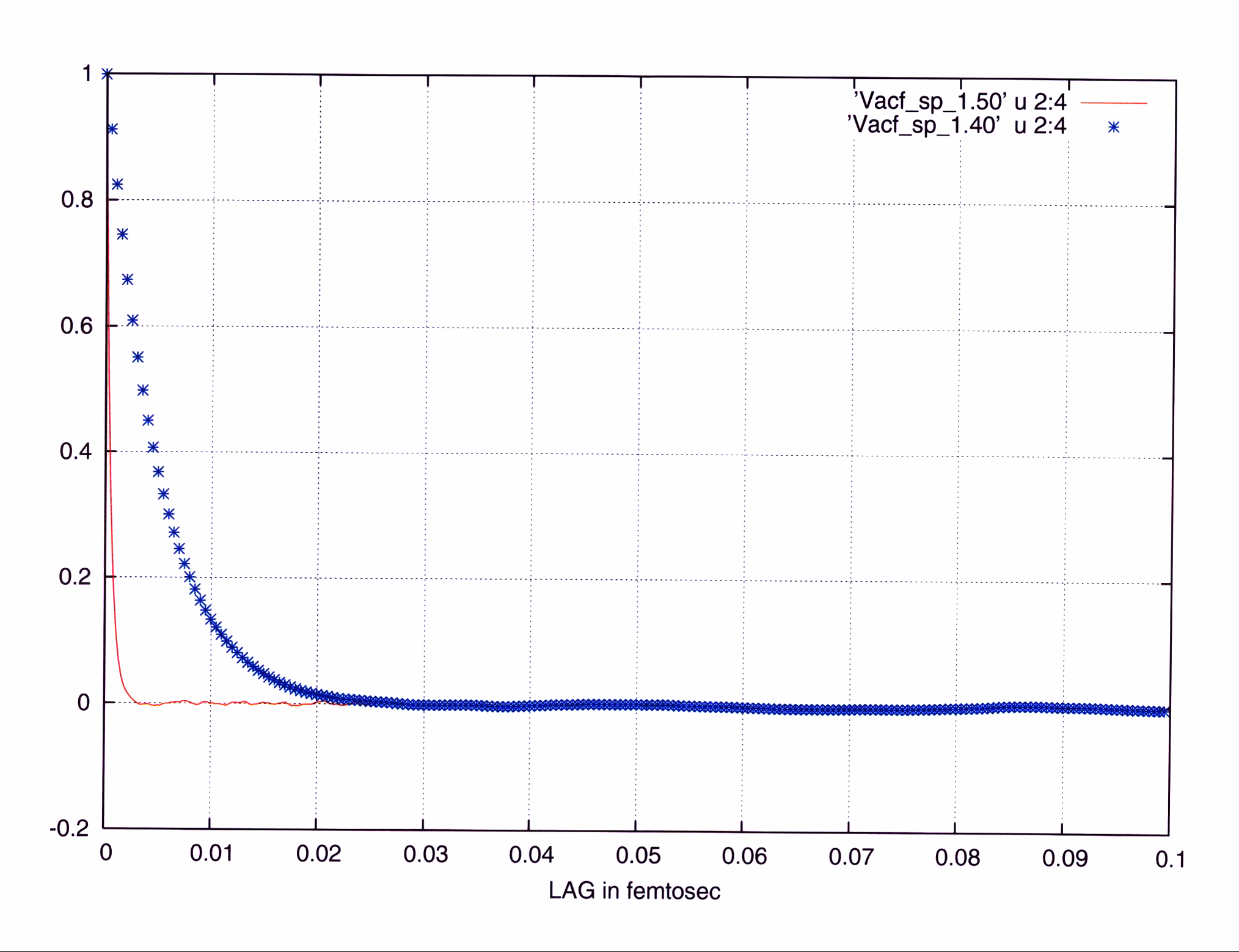
I attach two graphs. Corr1 presents the correlations for the two timesteps as a function of the ordinal numeric LAG. Corr2 presents as a function of time LAG, i.e. the numeric LAG was multiplied by the timestep. (40==5e-4, 50==5e-5)
Contrary to the expectations and common sense in the first one the correlations are identical while in the second one they differ by a factor of 10 (the ratio of the time steps).
What I am doing wrong ?