Dear Dr. Axel Kohlmeyer,
Hello Dr. Kohlmeyer. First, thank you so much for your many advice and suggestions on LAMMPS.
I currently have an equilibrated system of 100 polymer chains where each beads are connected by harmonic bonds with equilibrium distance being 0.97sigma (in LJ units). Non-connected beads are governed by attractive LJ potential and the 1-2 pairwise interaction (between bonded beads) are turned off. Initially, the polymer chains were created by random walk with a constant bond length of 0.97sigma, and I run it under NVE ensemble.
When I calculate the average bond length (from dump file) for the entire system of polymer chains at each timestep during the NVE run, I always obtain slightly less than 0.97*sigma. I should expect, for some timestep, I should obtain slightly larger and for other timestep, I should obtain slightly smaller than 0.97, but not always slightly less than the equilibrium length.
However, I always obtain slightly less than 0.97*sigma such as 0.9685, 0.9689, 0.9686 or 0.9688 etc.
I was curious if there is something in LAMMPS that is causing this.
I deeply appreciate for your time and effort.
Sincerely,
Masato Koizumi
P.S. If necessary, I attach my script
A_DPD_25_Timestep_50K.in (1.51 KB)
Is the system at pressure > 0? The more
the system is squeezed, the shorter
the bond lengths will be on average.
Steve
Dear Dr. Steve Plimpton,
Hello Dr. Plimpton. Thank you so much for your response.
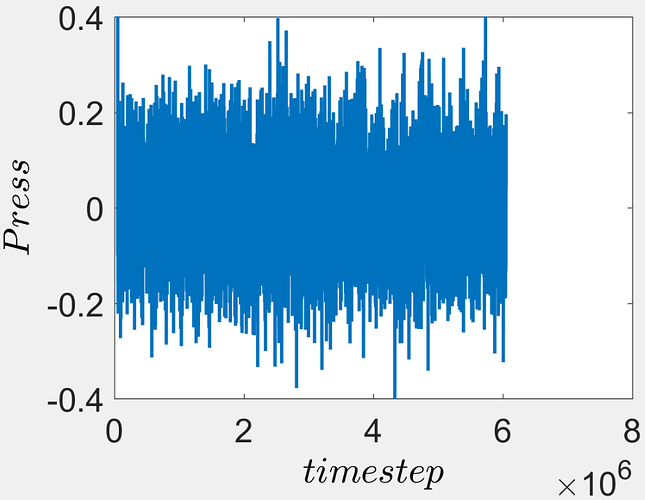
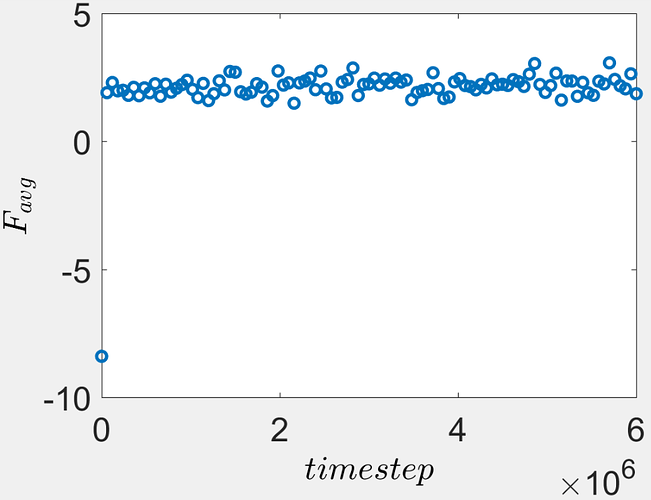
The system pressure fluctuates about zero as shown in the figure below. Therefore, the system is relaxed thereby the fixed volume under NVE ensemble is the equilibrated volume. Nevertheless, the average FENE bonds in the polymer chains (measured every 60000 timesteps) are slightly compressed as seen in the second figure. Furthermore, the average bonds were also slightly smaller than the pairwise equilibrium bond distance. (The force in each FENE bond was outputted by compute b2 all bond/local force.)
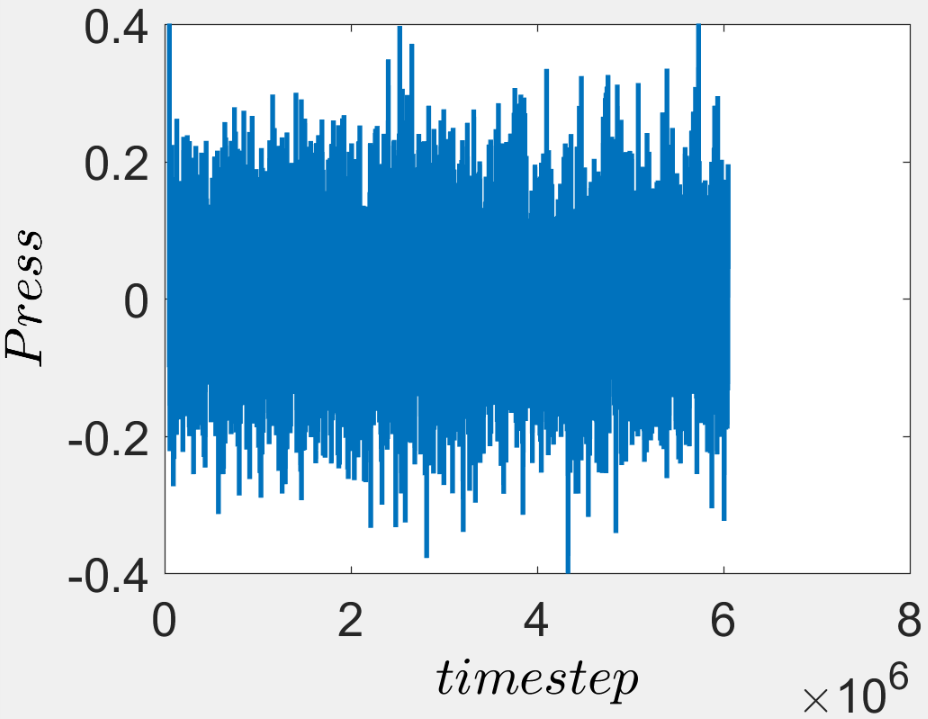
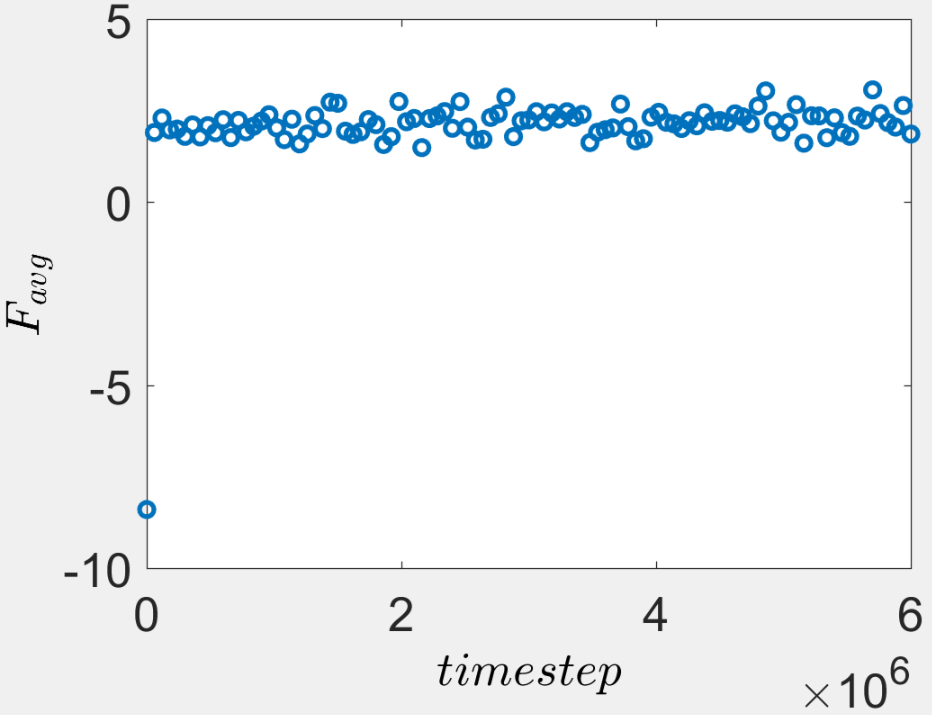
I have already tested the same case with NPT ensemble to confirm that the compressed FENE bonds are not a result of volume constraints. However, it seems that the FENE bonds are still compressed.
I am having trouble identifying the source of FENE bonds not relaxed even though the system is relaxed and the system potential energy have reached its minimum. I would greatly appreciate if I could request for any suggestions.
I have created a small (but large enough system such that the fluctuation is not as severe) LAMMPS code that replicates the issue of compressed FENE bonds under zero pressure (the simulation takes 26 minutes and outputs a total of 200 dumpfiles to accurately track the evolution of average bond force)
Once again, I deeply appreciate your time and effort.
Sincerely,
Masato Koizumi
A_DPD_25_Timestep_50K.in (1.38 KB)
polymer_10c10m.dat (9.76 KB)
In your first email you said harmonic bonds, which are symmetric.
Now you are saying FENE bonds, which are not. I don’t even
know if the minimum is exactly 0.97 or not. The delta
you are seeing is tiny. So I don’t know why you are concerned.
If the bond potential is non-harmonic and non-symmetric,
which FENE is, I don’t know why the average distance
should be exactly at the minimum.
Steve


Dear Dr. Steve Plimpton,
Hello Dr. Plimpton. Thank you for your response. I apologize for the confusion.
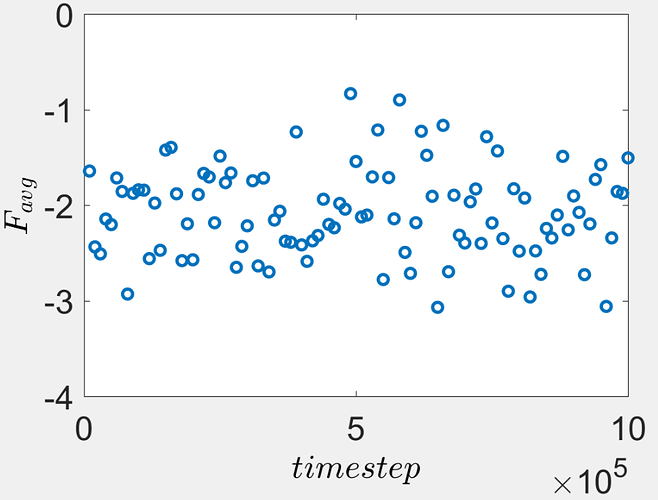
I was trying both harmonic and FENE. Even when the system pressure (in the x, y and z) is zero where all the bonds in my polymer chains (subject to NPT ensemble) are harmonic, I still see small compression. I averaged all the harmonic bond force in the polymer chains at designated timesteps (as shown below) and every averaged bond falls below zero (for symmetric harmonic potential)
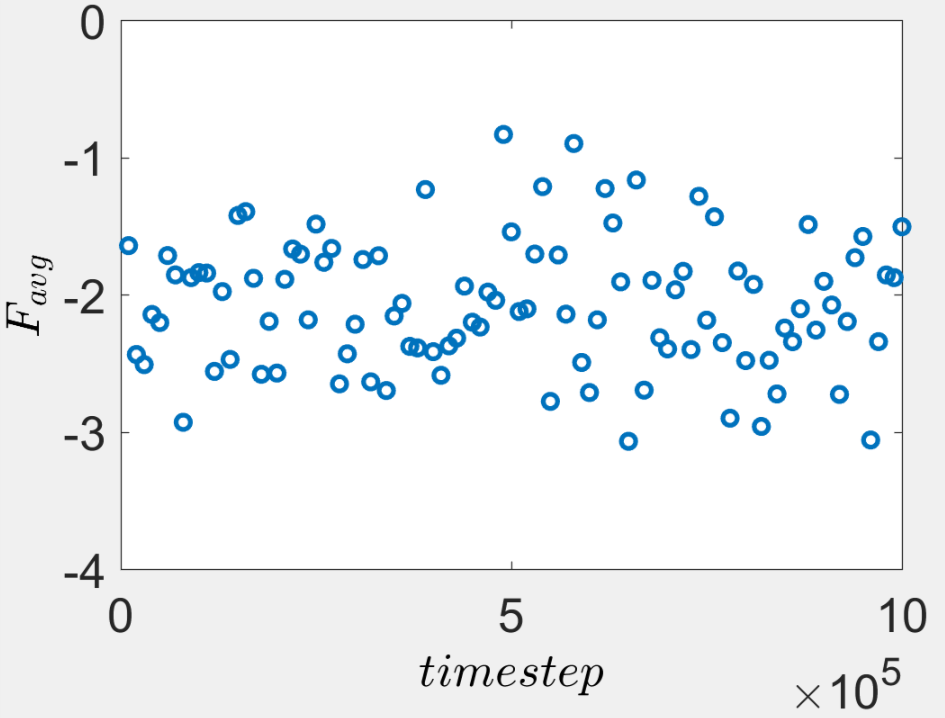
A tiny force implies that the system itself is not fully relaxed (pre-compressed). However, the second plot shows that the system is fully relaxed and the average pressure is zero with small numerical roundoff negligible compared to the offset I am seeing in the average bond force.
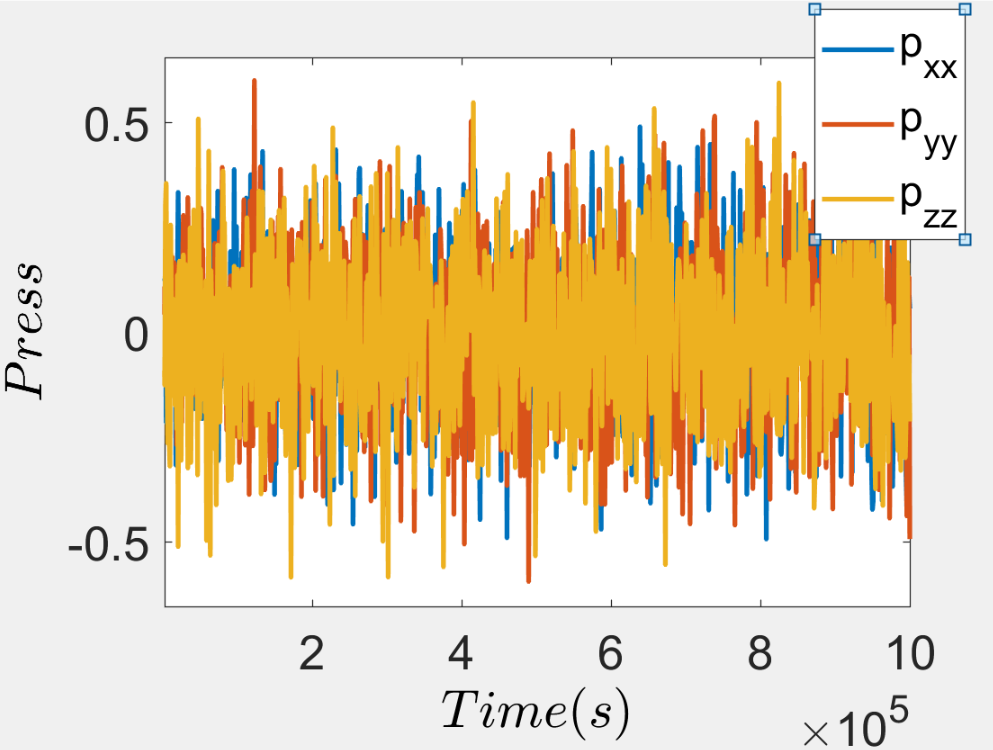
Also, for the case with asymmetric FENE bonds, even if the bond force is tiny, then I should see a small non-zero system pressure when I average. However, the average system pressure turns out to be very close to zero negligible compared to the compressed offset I am seeing with the bond force.
Another issue with my previous e-mail is that I am not sure why the FENE bonds would be compressed (even thought they are small). Looking at the structure of FENE potential, the bonds would rather be in tension since the FENE potential has a flatter region for bond length larger than the equilibrium distance and repulsive steep incline for bond length smaller than the equilibrium distance. Therefore, if there would be a small offset at relaxed state, then the averaged FENE bonds would rather choose tension (not compression) although very small.
The simulation is run under the NPT ensemble (or NVE ensemble with equilibrated volume).
I am thinking that there is something in my code that is universally causing a bias towards bond compression at relaxed state but having trouble identifying the source. I would greatly appreciate for any comments.
Once again, I am really thankful for all of your suggestions.
Sincerely,
Masato Koizumi


Sorry, I am out of ideas. Maybe someone else will respond.
Steve




Sorry, I am out of ideas. Maybe someone else will respond.
i don’t get the whole discussion. this is for condensed phase, not (low density) gas phase, so you cannot look at bonded interactions independently. the system will relax into a structure that is balancing bonded and non-bonded interactions, i.e. the total potential function. i have not seen a convincing argument in this discussion that requires that the equilibrium state of the total potential enforces to have the equilibrium state of each contributing component. to give an extreme example: please look at water where the equilibrium geometry in bulk is quite different from gas phase; in experiment and in simulation with a flexible water potential. thus only in (low density) gas phase, where the non-bonded contribution is very small, would i expect for a bead-spring system to have bonds in their individual equilibrium (and only if there are no other bonded interactions that couple to the bond motion, and the chains are not long enough to fold over and then have larger non-bonded contributions again).
axel.
Dear Dr. Axel Kohlmeyer,
Hello Dr. Kohlmeyer. I would like to deeply thank you for your advice.
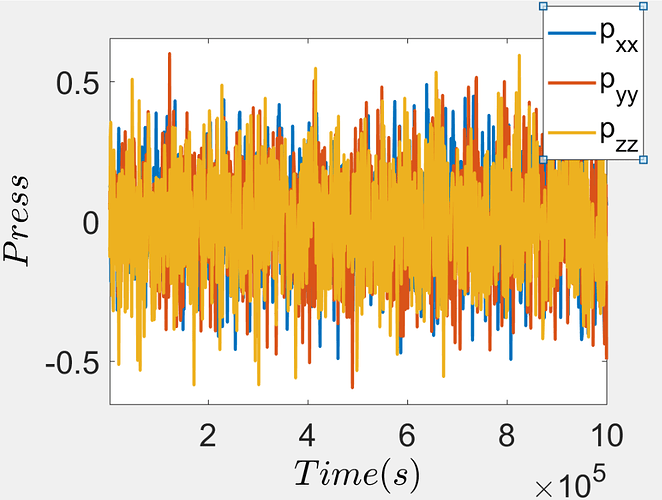
Yes, I agree that for condensed phase, the system will relax into a structure that is balancing bonded and non-bonded interactions and only when the non-bonded contribution is negligible would a bead-spring system will result in bonds settled in their individual equilibrium. In fact, when I plotted the system pressure, the pressure contributions from the non-bonded interactions and bonded interactions are non-zero and but they will sum to zero to realize overall relaxed system.
As you mentioned, this is a condensed phase where I have 100 chains each consisting of 100 beads with a high system density of 0.85. Therefore my condensed system is a polymer melt.
However, in a polymer melt, the long range interaction, or the non-connected LJ potential are screened out. That is, each bead to not feel any long range interactions since these non-bonded interactions are canceled out by surrounding chains. Therefore, the beads will feel the pairwise repulsive LJ plus the FENE potential acting between connecting beads.
If this is the case, should not the equilibrium state of the total potential be the same as the equilibrium state of each FENE bond? In other words, since the non-bonded interactions are screened out, should the equilibrium state of the polymer melt be similar to low density system in term of equilibrium of each component?
Once again, I am deeply grateful for your help during your busy schedule!
Sincerely,
Masato Koizumi