Hello everyone,
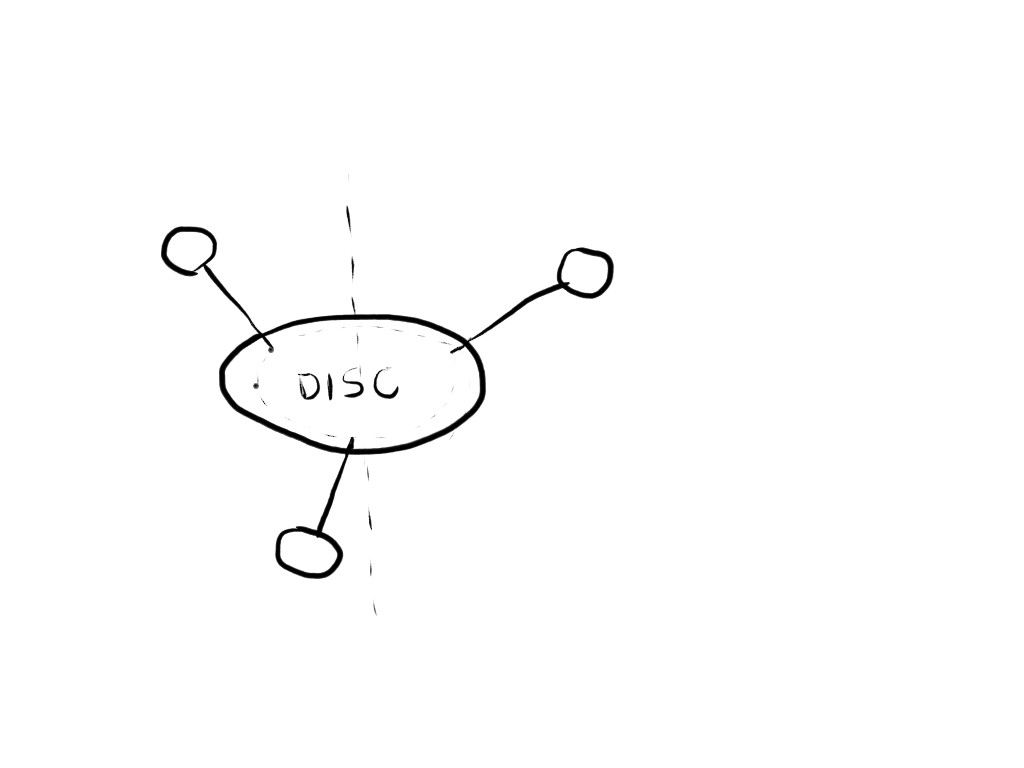
I'd like to implement a very specific model involving ellipsoids. I'm attempting to represent a molecule
using a central disc-like ellpisoid (highly oblate spheroid), with three radially-outward identical side bonds
which are equally spaced along and attached to the rim of the disc.
Now, as far as I understand, there is no exact way I can implement this in LAMMPS, as there is
no "disc boundary" in the ellipsoid definition, where I can attach the bonds. Also, if I attach the bonds
to the center of the ellipsoid, then the bonds wont exert any torque on the ellipsoid.
I'm wondering if I could define angle interactions between the side bonds and the axes of rotation of the ellipsoids.
This would enable me to mimic the effect of the bonds being attached to the rim of the disc instead of its center.
I understand this is more of a modelling question rather than a LAMMPS issue per se,
but I'd like to know what's possible. Hope my question makes sense. I have attached a
(poor) schematic of the same.
Anirban
Graduate Student
Rensselaer Polytechnic Institute
Hello everyone,
I'd like to implement a very specific model involving ellipsoids. I'm
attempting to represent a molecule
using a central disc-like ellpisoid (highly oblate spheroid), with three
radially-outward identical side bonds
which are equally spaced along and attached to the rim of the disc.
Now, as far as I understand, there is no exact way I can implement this
in LAMMPS, as there is
no "disc boundary" in the ellipsoid definition, where I can attach the
bonds. Also, if I attach the bonds
to the center of the ellipsoid, then the bonds wont exert any torque on
the ellipsoid.
I'm wondering if I could define angle interactions between the side
bonds and the axes of rotation of the ellipsoids.
This would enable me to mimic the effect of the bonds being attached to
the rim of the disc instead of its center.
I understand this is more of a modelling question rather than a LAMMPS
issue per se,
but I'd like to know what's possible. Hope my question makes sense. I
have attached a
(poor) schematic of the same.
Anirban
Graduate Student
Rensselaer Polytechnic Institute

Hello everyone,
I’d like to implement a very specific model involving ellipsoids. I’m
attempting to represent a molecule
using a central disc-like ellpisoid (highly oblate spheroid), with three
radially-outward identical side bonds
which are equally spaced along and attached to the rim of the disc.
Now, as far as I understand, there is no exact way I can implement this
in LAMMPS, as there is
no “disc boundary” in the ellipsoid definition, where I can attach the
bonds. Also, if I attach the bonds
to the center of the ellipsoid, then the bonds wont exert any torque on
the ellipsoid.
I’m wondering if I could define angle interactions between the side
bonds and the axes of rotation of the ellipsoids.
This would enable me to mimic the effect of the bonds being attached to
the rim of the disc instead of its center.
I understand this is more of a modelling question rather than a LAMMPS
issue per se,
but I’d like to know what’s possible. Hope my question makes sense. I
have attached a
(poor) schematic of the same.
How about approximating the ellipsoid with a collection of point particles and using a rigid integrator? You can then simply attach your bonds to 3 of those atoms. There should be some publication from Sharon glotzer’s group on how to do the expansion efficiently.
I'm also a bit concerned about the computational efficiency of these approaches. The ellipsoidal approach will allow me to use gay-berne potentials, which are expensive, but, on the other hand, rigid integrators can be expensive too. I'm really not sure which one is obviously cheaper.
Anirban
I'm also a bit concerned about the computational efficiency of these
approaches. The ellipsoidal approach will allow me to use gay-berne
potentials, which are expensive, but, on the other hand, rigid integrators
can be expensive too. I'm really not sure which one is obviously cheaper.
please let me know, how is an integrator for an extended particle is
different from a rigid integrator?
axel.
I also noticed I was comparing apples and oranges.
Using an ellipsoidal description will require me to use the gay-berne potential which is expensive,
but integrators for such an extended particle will not involve constraints.
On the other side, I was assuming that rigid body integrators will involve imposing constraints artificially
, which may have computational drawbacks. However, it seems from the manual that the lammps rigid
integrators don't do that.
So, using rigid body integrators seems to be an obvious choice, unless I'm making faulty assumptions again.
Anirban
Incidentally, there have been a couple posts requesting a feature
similar to the one you asked for. Here's one post:
http://lammps.sandia.gov/threads/msg30111.html
(click on the attached .png file at the bottom of the post)
I suppose it requires figuring out a small bit of math, and I don't
know if the demand is high enough to justify it. (And there are
other features higher on my wish list.) Anyway, I personally have
been following an approach similar to what Axel suggested,
representing the ellipsoid as a couple of atoms bonded together. (I
don't use rigid constraints or integrators, but it's the same idea.)
Cheers!
Andrew
Or you could create a rigid body which has the ellipsoid
and some additional (light) point particles to attach bonds
to. For 2 such particles, you attach bonds as desired, which
will induce force/torque on the rigid body. You can use the
GayBerne potential for ellipsoid/ellipsoid interactions, and
define no point/point interactions. Use fix rigid to integrate
the motion of the rigid bodies, or fix rigid/small.
Steve
