Hello everyone,
I have a question regarding the post prosses calculation of the elastic properties of a bulk polymeric glass system. We know from theory that the stress strain curve of epoxies has a linear part in small strain (up to 5%). I deform my system and I extract the data for the three tensile tests in the x,y,z directions and plot the stress strain curves. However not all plots pass throught the (0,0) point of the plot. My question is when I do the linear fit is it better to fit with:
- y = ax+b
- y = ax
See the figures below:
This is with the 1 type of fitting
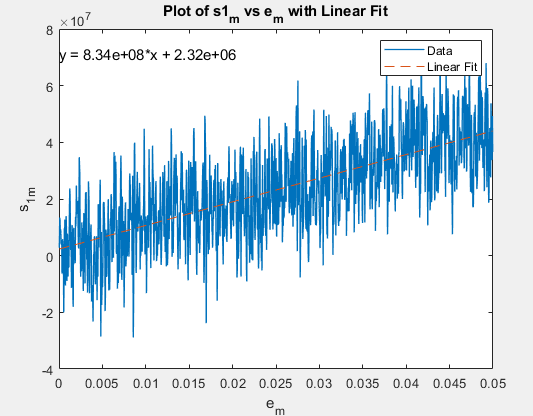
And this is the 2 type of fitting
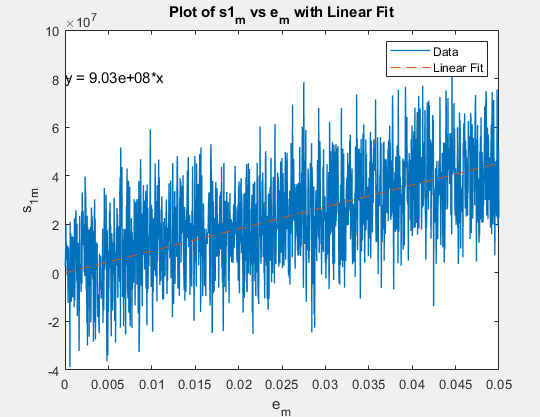
The first one gives a value of 0.84GPa and the second a value of 0.90GPa.
Thanks!
Hi @Iakovos_Delasoudas,
In the Science talk part of the forum, do not hesitate to mention which code and methods you use as it is not related to specific software. People using similar tools might be more eager to help you if they know what you are actually using and where issues might stem from.
I assume you are doing MD given previous interactions with had but correct me if I’m wrong here. That said, I think there are methodological questions to consider in your case. Here are some 2cts:
- Are these instantaneous values or averaged values over some period of time? Over which period? Tensile tests at the MD scales can be quite faster than experimental conditions which can result in large instantaneous fluctuations.
- Do you strain your systems with constant section? Only in this case is the relationship in elastic strains really linear.
- How reproducible are your results? An easy way to have an error bar is to perform your simulations several times and compute the standard deviation and error to the mean of your results.
Now when you say:
The computation of C_{ij} values uses relative strain \varepsilon but only relative to a reference state. The regression will pass through 0 stress value only if your reference state is actually 0 stress. And again, this 0 stress value is an ensemble value so you can have instantaneous finite stress in your reference state. It is possible to compute elastic constant of systems with finite stress.
A final thing you could do is to also perform compression of your system since your are likely to pass through the 0 stress point and check that your system is elastic in both strain regimes. In both case I would always fit using your first formula since the second one is only a special case where b is set to 0.

