Hello dear all,
I am trying to calculate the C matrix of a polymer network consisting of 256 BisF and 128 DETDA molecules with 85% crosslink density, well equilibrated for 100ns in the NPT ensemble at 300K. I use the Dreiding potential and so I have modified the init.mod and potential.mod files to mach the requirements of Dreiding. I am aware that calculating the C matrix in finite temperature is tricky and i have some questions about it.
-
As I have understant up to now the crucial parameters for computing correct the C matrix is the equilibration times after the small deformation (nequili as detonated in the script) and the length of equilibrated run (nrun as detonated in the scrip) and the up parameter that sould not alter the results if the model is converged.
-
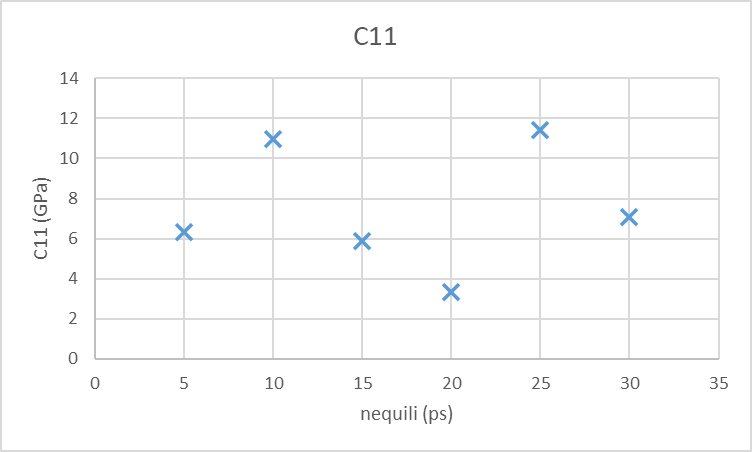
I tried to make a convergence study keeping the sampling time nrun and the variable up fixed (nrun = 10ps and up = 1e-2) and alter the nequili as 5,10,15,20,25,30 ps and see if the results converge. The timestep is 1fs. The C11 parameter calculates does not seem to converge at all and it is far away from the experimental value that is 4.1 GPa as you can see from the folowing system.
Do you have any suggestion on what is going wrong or what are the tricky parts that i sould wach out. As I have notticed the creator of the script @athomps answers a lot of questions about that so the aid will be well apriciated!
Thank you in advance for your time!
I will also upload my scripts for nequili = 10ps
ELASTIC_T_eq100.rar (2.7 MB)
Just a quick note. .rar style archives are very difficult to handle for people not running on Windows. Most LAMMPS developers use Linux and there .tar.gz is the preferred format for archives.
Yes you are righ Axel! Thanks for the note. Here is the file in .tar.gz
ELASTIC_T_eq100.tar.gz (3.0 MB)
Hi @Iakovos_Delasoudas,
Computing elastic constant with static NVT strains the way the original example of ELASTIC_T does is tricky for polymeric systems. The reason is because there is still room for stress relaxation through molecular reorganization with small strains because if the network is not fixed. See this as a compressive part of your system that can get squeezed and absorb the stress. So if the network is not very highly cross-linked you can get surprising results. Such computation are not that straight forward at finite temperature as you said.
Also the most important parameter is the convergence of your average stress values. You should plot them with error bars and see if you are in the elastic regime of a solid-like behavior. This is not straight forward from the example. You might do some separate runs at several strains from the same initial configuration and see that yourself. More details in one of our previous paper here.
Alternatively the fluctuation stress method at the end of the paper has been implemented last year in LAMMPS. You can use the born/matrix compute command and get the full C_{ij} tensor in one go. You also need to compute the virial stress tensor at each step and compute the covariance of each terms. The Born matrix terms add some computation time to each time step but it converges rather quickly. The virial stress covariance on the other hand needs way more terms (approx. a million depending on the system), but does not add much computation at each steps. You can find a example scripts in the ELASTIC_T/BORN_MATRIX directory of the LAMMPS repository.
Please see more details on the fluctuation implementation method in our previous work with Aidan here.
2 Likes
Dear Mr. Clavier, @Germain
Thank you for your imediate and very helpfull answer. I will try to modify the BORN_MATRIX input so it fits with my system if this is possible. Do you think that this is more apropriate for a polymeric system? I allso checked the paper you mention and I have a simple computational question. (I am quite new in the field of statistical mechanics)
In the Ray & Rahman equation for the calculation of the ε matrix through the equation
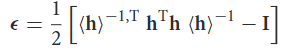
the < h > is the average of the scaling matrix up to the step that you calculate ε and the h is the tensor in the curent step? Im I correct? I suppose the algorithm for example for the C_11 component goes like:
- Run a long MD simulation under NPT with small deformation in x direction and compute the ε tensor from the above equation. Save the h components to compute the averages
- Compute hte averages <ε11> <ε11> and <ε11ε11> and compute the C_1111
Thank you in advance
No. The \langle \mathbf{h} \rangle matrix is the ensemble average and \mathbf{h} are instantaneous values. This is because in the NPT ensemble you are interested in instantaneous deviation from ensemble average to define instantaneous strain values.
This is also incorrect. You do not perform deformations in the NPT ensemble as the box is allowed to change to relax the stress. The only data you need are box coordinates (l_x, l_y, l_z, xy etc.) to compute the average and instantaneous \mathbf{h} matrices. The C tensor is directly obtained by computing the covariance of the \varepsilon tensor and taking the inverse (with some multiplicative factor).
However from experience I would not recommend using this method with standard molecular dynamics simulation (i.e. Nosé-Hoover barostat). It is known to be “slow to converge” and in the first paper I linked, we showed that convergence is very sensitive to the coupling parameter (barostat mass). I’ve never seen it giving comparable results with NVT methods. It does work with NPT monte-carlo simulations as far as I can tell but I could verify this with the code presented in the paper which is under a proprietary license.
So in the expression I mentioned I calculate the instantaneous values of ε tensor and then I use them to compute the ensemble averages <ε11> <ε11> and <ε11 ε11> ?
So I just deform and then relax the system in the NPT and compute the ensemble averages above?
So will you recomend NVT?
This is a way of phrasing it, yes.
This makes no sense.
Yes.
Thanks a lot for your comments!
Good morning dear sir @Germain ,
I followed your instructions (I hope so) and I used the NVT ensamble with the Born Matrix formula by modifying the existing script ELASTIC_BORN_MATRIX to fit my systems potential and units. I think I have correctry trqansfornmed the units from metal to real and I used an averaging run of 10ns. The initial geometry is an epoxy network well equilibraded for 100ns under NPT ensemble. The results are quite unusual. Can you suggest a reason why? I attach my files and results. (log.elastic.ortho)
Thank you!
ELASTIC_BORN_MATRIX.tar.gz (1.5 MB)