Hello LAMMPS Users,
I would like to compute the dihedral angle of each of the individual backbone dihedrals present in my system with respect to all the time frames. I need this to check the dihedral transitions.
I would like to know if its possible in LAMMPS?
If yes, then which command can be used for this.
I would be grateful for any suggestions.
Thank you,
Sanjeet
This is a post-processing task. You should look into tools for analyzing MD simulations. Some are listed here: Pre/Post Processing Tools for use with LAMMPS
Dear Axel,
Thank you for your comment.
Hello Sanjeet,
You can also easily do a python code to calculate this. Suppose that you read your entire trajectory and transform it into an array containing L x N lines (L being the number of microstates and N being the amount of atoms in your system) and 5 columns (assuming you have one column for atom-ID, atom type and the three coordinates). Suppose also that you read the dihedral angle section of your system and transform it into an array with D lines (D being the number of dihedrals you have declared in the .data file) and 6 columns (dihedral-ID, dihedral-type, and the following 4 atom-IDs).
Then, for each frame individually, you could calculate the dihedral angle as follows:
# dihedral angle section: D x 6 array.
# A: one snapshot of the trajectory, so a N x 5 array.
for it_1 in range (0, len(dihedral_angle_section)):
CG_atom_i_ID = dihedral_angle_section[it_1,2]
CG_atom_j_ID = dihedral_angle_section[it_1,3]
CG_atom_k_ID = dihedral_angle_section[it_1,4]
for it_2 in range(0, NA):
if A[it_2,0] == CG_atom_i_ID:
position_CG_atom_i = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
if A[it_2,0] == CG_atom_j_ID:
position_CG_atom_j = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
if A[it_2,0] == CG_atom_k_ID:
position_CG_atom_k = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
dist_x_j_i = position_CG_atom_i[0,0] - position_CG_atom_j[0,0]
dist_y_j_i = position_CG_atom_i[0,1] - position_CG_atom_j[0,1]
dist_z_j_i = position_CG_atom_i[0,2] - position_CG_atom_j[0,2]
if (abs(dist_z_j_i) > abs(((k[0,2])/2))) & (dist_z_j_i > 0) :
position_CG_atom_i[0,2] = position_CG_atom_i[0,2] - k[0,2]
if (abs(dist_z_j_i) > abs(((k[0,2])/2))) & (dist_z_j_i < 0) :
position_CG_atom_i[0,2] = position_CG_atom_i[0,2] + k[0,2]
if (abs(dist_x_j_i) > abs(((mod_i)/2))) & (dist_x_j_i > 0) :
position_CG_atom_i[0,0] = position_CG_atom_i[0,0]- i[0,0]
if (abs(dist_x_j_i) > abs(((mod_i)/2))) & (dist_x_j_i < 0):
position_CG_atom_i[0,0] = position_CG_atom_i[0,0] + i[0,0]
if (abs(dist_y_j_i) > abs(((mod_j)/2))) & (dist_y_j_i > 0) :
position_CG_atom_i[0,1] = position_CG_atom_i[0,1] - j[0,1]
if (abs(dist_y_j_i) > abs(((mod_j)/2))) & (dist_y_j_i < 0):
position_CG_atom_i[0,1] = position_CG_atom_i[0,1] + j[0,1]
dist_x_j_k = position_CG_atom_k[0,0] - position_CG_atom_j[0,0]
dist_y_j_k = position_CG_atom_k[0,1] - position_CG_atom_j[0,1]
dist_z_j_k = position_CG_atom_k[0,2] - position_CG_atom_j[0,2]
if (abs(dist_z_j_k) > abs(((k[0,2])/2))) & (dist_z_j_k > 0) :
position_CG_atom_k[0,2] = position_CG_atom_k[0,2] - k[0,2]
if (abs(dist_z_j_k) > abs(((k[0,2])/2))) & (dist_z_j_k < 0) :
position_CG_atom_k[0,2] = position_CG_atom_k[0,2] + k[0,2]
if (abs(dist_x_j_k) > abs(((mod_i)/2))) & (dist_x_j_k > 0) :
position_CG_atom_k[0,0] = position_CG_atom_k[0,0] - i[0,0]
if (abs(dist_x_j_k) > abs(((mod_i)/2))) & (dist_x_j_k < 0):
position_CG_atom_k[0,0] = position_CG_atom_k[0,0] + i[0,0]
if (abs(dist_y_j_k) > abs(((mod_j)/2))) & (dist_y_j_k > 0) :
position_CG_atom_k[0,1] = position_CG_atom_k[0,1] - j[0,1]
if (abs(dist_y_j_k) > abs(((mod_j)/2))) & (dist_y_j_k < 0):
position_CG_atom_k[0,1] = position_CG_atom_k[0,1] + j[0,1]
vector_u = position_CG_atom_i - position_CG_atom_j
vector_v = position_CG_atom_k - position_CG_atom_j
normal_vector_plane_1 = np.cross(vector_u, vector_v)
# -----------------------------------------------------------------------
# Now for the second plane (I will continue with the nomenclature i, j, k instead of switching to j, k, l, but this doesnt matter):
CG_atom_i_ID = dihedral_angle_section[it_1,3]
CG_atom_j_ID = dihedral_angle_section[it_1,4]
CG_atom_k_ID = dihedral_angle_section[it_1,5]
for it_2 in range(0, NA):
if A[it_2,0] == CG_atom_i_ID:
position_CG_atom_i = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
if A[it_2,0] == CG_atom_j_ID:
position_CG_atom_j = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
if A[it_2,0] == CG_atom_k_ID:
position_CG_atom_k = np.array([[A[it_2,2], A[it_2,3], A[it_2,4]]])
dist_x_j_i = position_CG_atom_i[0,0] - position_CG_atom_j[0,0]
dist_y_j_i = position_CG_atom_i[0,1] - position_CG_atom_j[0,1]
dist_z_j_i = position_CG_atom_i[0,2] - position_CG_atom_j[0,2]
if (abs(dist_z_j_i) > abs(((k[0,2])/2))) & (dist_z_j_i > 0) :
position_CG_atom_i[0,2] = position_CG_atom_i[0,2] - k[0,2]
if (abs(dist_z_j_i) > abs(((k[0,2])/2))) & (dist_z_j_i < 0) :
position_CG_atom_i[0,2] = position_CG_atom_i[0,2] + k[0,2]
if (abs(dist_x_j_i) > abs(((mod_i)/2))) & (dist_x_j_i > 0) :
position_CG_atom_i[0,0] = position_CG_atom_i[0,0]- i[0,0]
if (abs(dist_x_j_i) > abs(((mod_i)/2))) & (dist_x_j_i < 0):
position_CG_atom_i[0,0] = position_CG_atom_i[0,0] + i[0,0]
if (abs(dist_y_j_i) > abs(((mod_j)/2))) & (dist_y_j_i > 0) :
position_CG_atom_i[0,1] = position_CG_atom_i[0,1] - j[0,1]
if (abs(dist_y_j_i) > abs(((mod_j)/2))) & (dist_y_j_i < 0):
position_CG_atom_i[0,1] = position_CG_atom_i[0,1] + j[0,1]
dist_x_j_k = position_CG_atom_k[0,0] - position_CG_atom_j[0,0]
dist_y_j_k = position_CG_atom_k[0,1] - position_CG_atom_j[0,1]
dist_z_j_k = position_CG_atom_k[0,2] - position_CG_atom_j[0,2]
if (abs(dist_z_j_k) > abs(((k[0,2])/2))) & (dist_z_j_k > 0) :
position_CG_atom_k[0,2] = position_CG_atom_k[0,2] - k[0,2]
if (abs(dist_z_j_k) > abs(((k[0,2])/2))) & (dist_z_j_k < 0) :
position_CG_atom_k[0,2] = position_CG_atom_k[0,2] + k[0,2]
if (abs(dist_x_j_k) > abs(((i[0,0])/2))) & (dist_x_j_k > 0) :
position_CG_atom_k[0,0] = position_CG_atom_k[0,0] - i[0,0]
if (abs(dist_x_j_k) > abs(((i[0,0])/2))) & (dist_x_j_k < 0):
position_CG_atom_k[0,0] = position_CG_atom_k[0,0] + i[0,0]
if (abs(dist_y_j_k) > abs(((j[0,1])/2))) & (dist_y_j_k > 0) :
position_CG_atom_k[0,1] = position_CG_atom_k[0,1] - j[0,1]
if (abs(dist_y_j_k) > abs(((j[0,1])/2))) & (dist_y_j_k < 0):
position_CG_atom_k[0,1] = position_CG_atom_k[0,1] + j[0,1]
vector_u = position_CG_atom_i - position_CG_atom_j
vector_v = position_CG_atom_k - position_CG_atom_j
normal_vector_plane_2 = np.cross(vector_u, vector_v)
mod_normal_vector_plane_2 = (normal_vector_plane_2[0,0]**2 + normal_vector_plane_2[0,1]**2 + normal_vector_plane_2[0,2]**2)**(1/2)
mod_normal_vector_plane_1 = (normal_vector_plane_1[0,0]**2 + normal_vector_plane_1[0,1]**2 + normal_vector_plane_1[0,2]**2)**(1/2)
cos_value = (normal_vector_plane_2[0,0]*normal_vector_plane_1[0,0] + normal_vector_plane_2[0,1]*normal_vector_plane_1[0,1] + normal_vector_plane_2[0,2]*normal_vector_plane_1[0,2])/(mod_normal_vector_plane_2*mod_normal_vector_plane_1)
angle_value = math.acos(cos_value)*180/(math.pi)
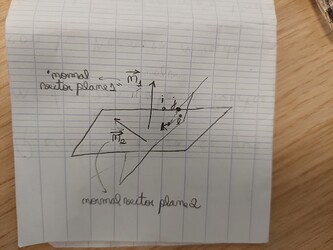
Assisted by some knowledge in analytical geometry (dot product and cross product basically), I think you can easily understand what the code is doing. I leave a drawing that may be useful as guidance to understand the code. You only need to create yourself a way to store these angle values of each dihedral in an histogram or something. And beware, because you always have two angles between the plane: X and 180 - X (i.e., you can measure the angle X or its supplementary angle)
PS: note that I am addresing the periodic boundary conditions (in case bonded atoms find themselves at different edges of the box) for an orthogonal box, so this you need to change accordingly depending on the geometry of your system.
Hello Cecilia,
Thank you so much for this!!
Cheers,
Sanjeet
FWIW, trajectories in YAML format are particularly easy to read into python.
https://docs.lammps.org/dump.html
https://docs.lammps.org/Howto_structured_data.html
Dear Sanjeet,
The best command for your purpose is “compute dihedral/local”.
Define a group comprising the backbone and use it with this compute.
The dihedrals calculated with this compute may be written to a separate
dump, as explained in documentation to “compute dihedral/local”.
Best regards,
Anders
Ahh, cool ^^
I will read about it for my next time with python + trajectories. I always write the trajectories in the usual (?) dump format because it is the only one I know 
Thanks
Dear Anders,
Thank you for your reply. I will try this.
Cheers,
Sanjeet
