Dear answerer, hello. I used LAMMPS to simulate a water droplet system (LAMMPS data file via write_data, version 2 Aug 2023, timestep = 20000, units = real)and intended to calculate its surface tension using the Irving-Kirkwood pressure tensor method. The calculation process is as follows:
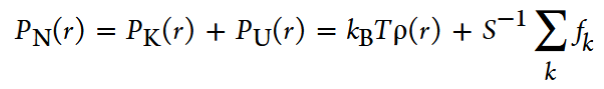
The normal component of the Ivring−Kirkwood pressure tensor, PN(r), which consists of kinetic and configuration terms,where kB is the Boltzmann constant, T is the temperature of the system, S is the surface area of the sphere with radius r, and fk is the component of the pairwise force orthogonal to the surface.
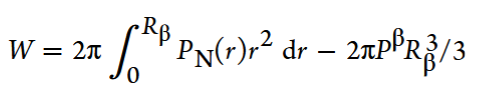
where Pβ is the vapor pressure and Rβ is a radius in the vapor region where PN(r) equals Pβ.
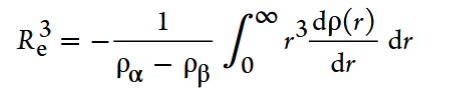
ρα and ρβ are the densities of the liquid and vapor.Finally, the surface tension is evaluated as
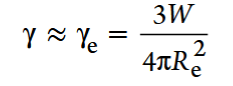
According to the results of my simulation, the output columns include the position of the center of the spherical shell, the number density, Pkrr Pkθθ Pkφφ Pvrr Pvθθ Pvφφ, a total of 8 columns of data. May I ask what is the relationship between the output data and PN(r)?
The purpose of this forum is to address questions specifically related to LAMMPS. While you might be using LAMMPS for your calculations, your question is more about physics than about LAMMPS itself. You might consider seeking assistance on a physics-focused forum.
PN(r) is normal to the interface. You need to determine which component that corresponds to from the geometry of your simulation. You get the pressure by summing the kinetic and virial terms of each component, e.g. Prr = Pkrr + Pvrr
Thank you very much for your reply. Your reply is very helpful for my research. However, when I was calculating, I found that the unit conversion seems incorrect. I have consulted the LAMMPS manual. For style real, the units pressure = atmospheres. Is the unit of the output data Prr in atmospheres (i.e., atm)? I’m not sure if my understanding is correct.
For real style yes the output data for pressure is in atm, see units command — LAMMPS documentation.
Thank you for your reply. Wish you a happy life!
Hello. According to your reply, PN(r)=Prr = Pkrr + Pvrr. So, does the calculation here only include the radial component and not the angular component? However, in the Irving - Kirkwood pressure - tensor method, PN(r) = PK(r) + PU(r) = kBT (r) + S−1 ∑ k fk. As far as I understand, all components should be decomposed into radial components. So I’m not quite sure what the differences betweenPkrr andPK(r) , and between Pvrr and PU(r) are. What’s the relationship between them? Before this, I used the formula PN(r)=Prr = Pkrr + Pvrr to calculate the normal component PN(r) of the pressure tensor and found that the final result was very different from the literature value, which led to the above questions.
So, does the calculation here only include the radial component and not the angular component?
It includes what is listed here: compute stress/cylinder command — LAMMPS documentation