Dear lammps users,
I'm trying to study buckling of thermally fluctuating membranes. The
in-plane stiffness is achieved by bonding the points (atoms) and the bending
is achieved by defining dihedrals. I have periodic boundary conditions as
well.
I need to study the behavior for various values of bond stiffness (K).
Consequently, I need to use a timestep that gives correct dynamics for
different stiffness values. If I'm not mistaken, the correct way is to first
calculate the smallest vibrational period of the system. So my first
question is:
1- Is it possible in LAMMPS to calculate the vibrational frequencies
(periods) to get the smallest period of my system and then calculate the
timestep? (basically eigenvalue analysis).
this is overkill. take hold of a proper text book on MD and look up
energy conservation.
that is for most systems a good measure to determine a suitable time
step. also, look up publications using the same force field on the
same or a similar system. this information is usually transferable.
The stiffest interaction and the lightest atoms set the upper limit
for the time step. if you can time integrate those with sufficient
energy conservation after equilibration and without a thermostat
you've found the right setting. for all atom simulations containing
hydrogen atoms this is often between 0.25 and 0.5 fs for systems
without contraints and 1fs to 2fs for constraining the hydrogen bonds
with fix shake. for systems, that only have heavier atoms,
correspondingly larger (scaling with sqrt(m) for smallest mass, if
memory servers me right).
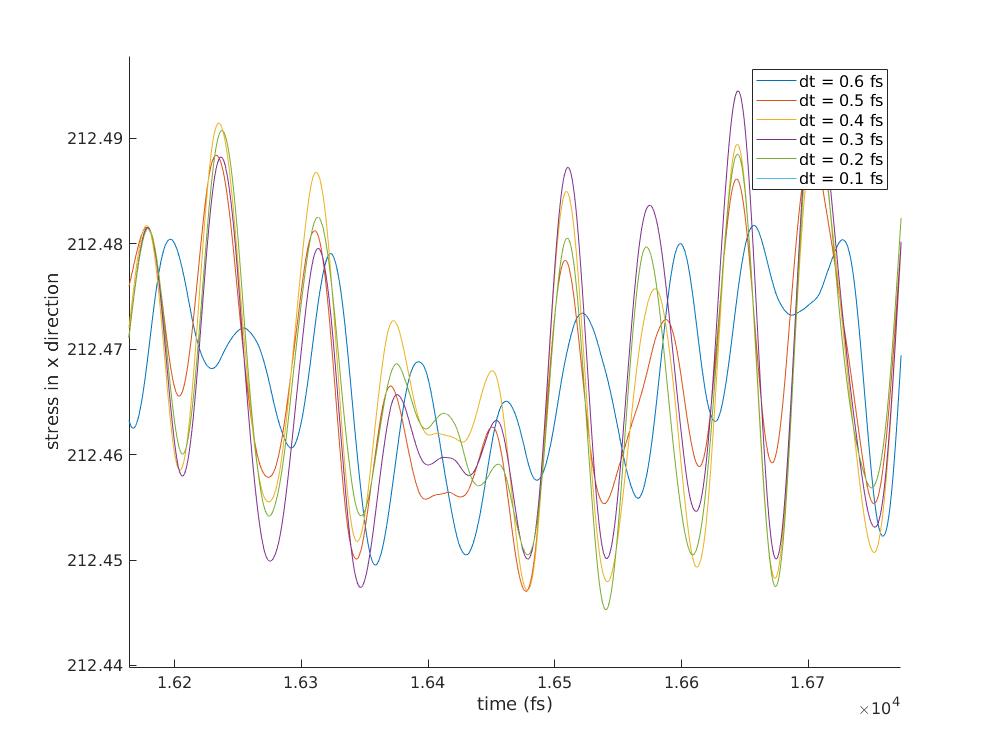
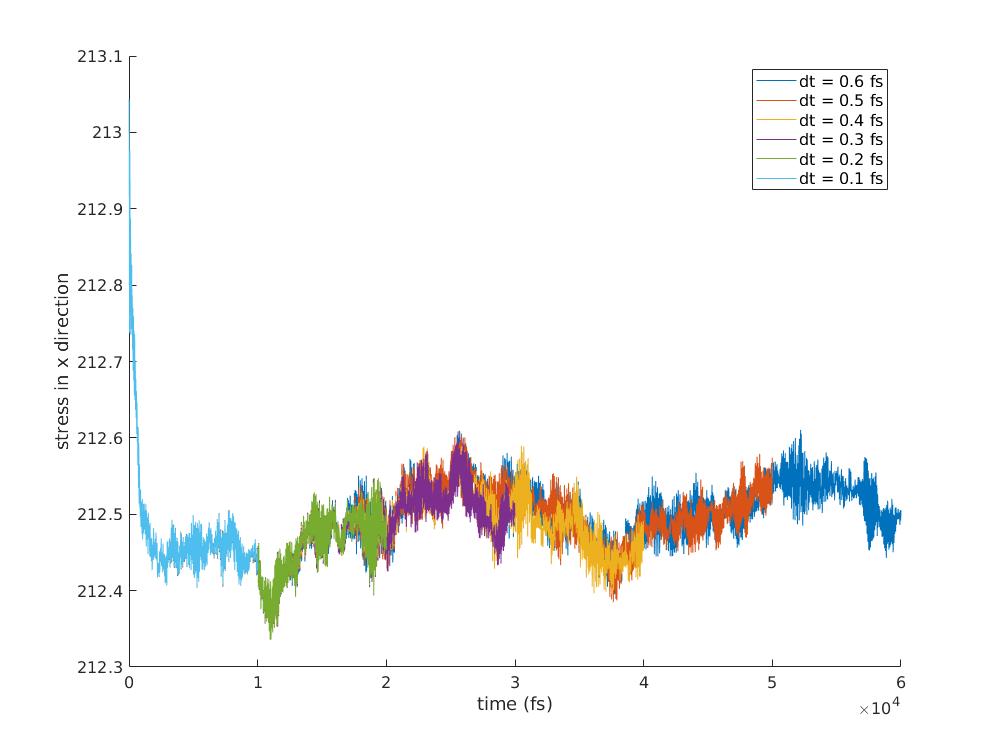
As suggested in other posts, I have tried different timesteps for the same
system (same velociy seed). I expected to see the same dynamics. Although
the general behavior is the same for different timesteps, they are not
exactly the same. So my second question is:
2- Do we expect to see exactly the same dynamics for systems that have been
run with different timestep or a general agreement would suffice?
again, please consult an MD text book for explaining what is
acceptable and not. please note, that due to using floating point math
and due to floatingpoint math being not associative, even using a
different number of processors, or having a different ordering of the
atoms (e.g. through a different neighbor list update interval),
trajectories can diverge.
I'm attaching parts of the datafile, runfile and two graphs. The graphs are
stress as a function of time for different timesteps. One graph is just the
zoomed in version of the other.
please note, that you are asking questions about the general nature of
MD and nothing that is particular to LAMMPS, and thus your inquiry is
a) mostly off-topic and b) is something that you should have learned
about *before* starting MD simulations and should discuss with your
adviser/tutor not this mailing list. there is much more to be learned
and a mailing list is a poor substitute for a proper tutor (and people
responding on mailing lists get tired having to explain stuff over and
over again, that is well explained in the basic text book literature).
axel.