Chunk/atom bin/2d

LAMMPS LAMMPS General Discussion
1

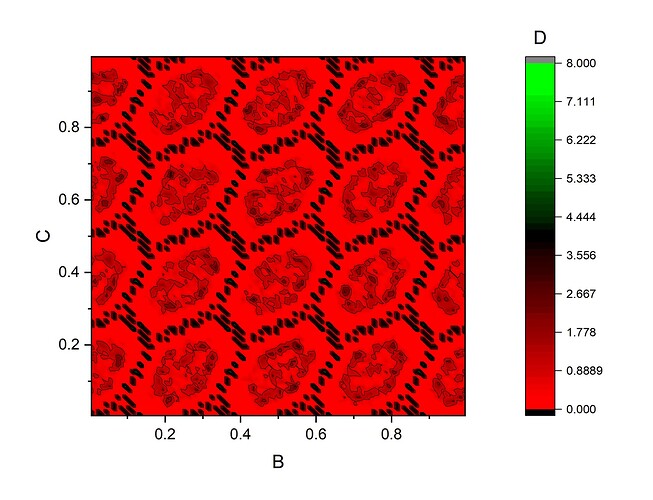
Hello everyone,
I am trying to plot a density map for my water adsorption simulation in MOF-74 (triclinic structure). For that I used:
unit real
…
compute water_local all chunk/atom bin/2d y lower 0.01 z lower 0.01 units reduced

and i got the map as below. The plot looks fairly accurate except the fact that the plot can not prove that the framework used for adsorption is tilted.

Can anyone help me with that?

Thank you,

Regards
Bishwas

74

433994172_744521127448946_8680626198814022329_n
433994172_744521127448946_8680626198814022329_n1920×1470 219 KB

2

Hi @Bishwas,

This is because of the way you plot your output data. As specified in the documentation of compute chunk/atoms:

For orthogonal simulation boxes, the bins are layers, pencils, or boxes aligned with the xyz coordinate axes. For triclinic (non-orthogonal) simulation boxes, the bin faces are parallel to the tilted faces of the simulation box. See the Howto triclinic page for a discussion of the geometry of triclinic boxes in LAMMPS. As described there, a tilted simulation box has edge vectors \overrightarrow{a}, \overrightarrow{b} and \overrightarrow{c}. In that nomenclature, bins in the x dimension have faces with normals in the \overrightarrow{b}\times\overrightarrow{c} direction, bins in y have faces normal to the \overrightarrow{a}\times\overrightarrow{c} direction, and bins in z have faces normal to the \overrightarrow{a}\times\overrightarrow{b} direction. Note that in order to define the size and position of these bins in an unambiguous fashion, the units option must be set to reduced when using a triclinic simulation box, as noted below.

It is then up to you to transform the coordinates of your plot to match the geometry of your simulation box, which seems to be the easiest solution to set up in your situation.

2 Likes
3

Thank you for your reply sir @Germain .

I am using a bin size of 0.01 in 2d so I have like 10000 data, can you please suggest fastest way to transform the coordinates of the plot in accordance to my MOF?

Thank you.

Bishwas

4

I do not know which software you are using to plot your data and the geometry of you simulation box. So no, I can’t be of much help expect telling you that it will involve computing a transformation matrix to go from the orthogonal plane to your simulation box shape.

The how-to triclinic section of the manual might be a good place to start.

1 Like
5

@Germain,
Thank you for your help.

Bishwas