I want to calculate dielectric constant variation with the time of charged particles that are perturbed initially by an electric field. The sea of charged particles consists of point particles with charge ‘q’ that are moving under periodic boundary conditions. I have researched a bit on how to calculate the dielectric constant using the dipole moment, but I am not sure if that is correct for my system. Could you please comment on that?
Your approach will not likely work. Computing the dielectric constant from MD simulations requires very long simulations in equilibrium to get converged results of the auto-correlation function for the total dipole moment, which would need to be inserted into the proper fluctuation formula.
I’ve worked on computing the dielectric constant for water molecules some 20+ years ago.
Please have a look at slides 18 to 21 of the following talk slides
talk-trieste2004.pdf (1.1 MB)
More details are in my PhD thesis, which is written in German, though. There are likely more recent publications on the subject.
Thank you for your reply. I looked at your slides and found them helpful. I have looked into the Neumann paper which describes how to find dipole moments in different geometry. I have a question about the differences in our systems. As you have used water molecules for simulation, I am using point particles with some charge ‘q’ and mass ‘m’. All of them have the same properties. As I understand dipole is two opposite charges separated by a distance, therefore, in my system there are fundamentally no dipoles (since all have the same charge). Can I still find the total dipole moment and its squared fluctuations from simulations and use it to calculate the dielectric constant?
PS: It would be really wonderful if you could share your thesis or references from it.
This is an unphysical system. It would have infinite energy due to periodic boundaries, if the charge-charge interactions are treated correctly.
This is a dipole, but also systems with more charge points can have a “dipole moment”. Please have a look at a text book on electrostatics.
The total dipole moment is not well defined for systems with a net charge.
You cannot calculate a dielectric constant for a non-neutral system.
Here is a PDF of my thesis. Please keep in mind that this is representing the state of the art from about 25 years ago. And some of the most instructive publications go back another 15-30 years before that, like the text book from Boettcher on Electric Polarization or the papers from Neumann and Steinhauser, or from Madden.
ak-phd-thesis.pdf (1.5 MB)
I have never met anyone who wants to calculate the electric response of a charge sea, and I think that includes you. What is the real-world system you want to model, and under what conditions? If you read Allen and Tildesley’s Computer Simulations of Liquids you will not go far before meeting this diagram:
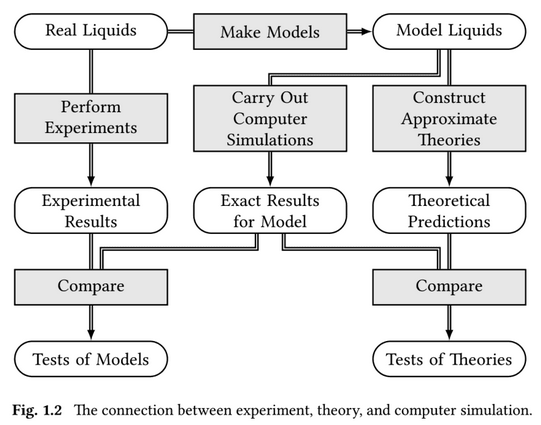
MD simulations are only useful for calculating quantities we can measure in real experiments and explain with understandable models. I don’t understand what the “dielectric constant” is of a charge sea, because a charge sea isn’t a dielectric! It’s an electrical conductor! An infinite charge sea doesn’t have a static equilibrium response to an electric field – only a non-equilibrium steady state, namely a constant current at which the electrical power input equals the thermal dissipative output.
So you have to find a model which does make sense, and for that you should go back to what real-world liquid you are trying to describe and under what circumstances.
Thank you for providing me with your thesis. I shall look at it in detail, and more into electrostatics.
I work in simulating complex plasma systems. In general, plasma have a dielectric constant and so does the complex plasmas. However, when simulating the complex plasmas I simulate only the complex part keeping the electron-ion plasma in the background via some potential (screened-coulomb). So I was wondering, if I can get a dielectric constant in such simulations, as simulating a three component plasma will take a lot more computational time and space.
Since you are not simulating the electrons, you cannot get the electron density distribution. However that would be required to compute the total dipole of your system.
That said, I am not certain that the fluctuation formula derived for charged point particles with either unscreened Coulomb or lattice-sum Coulomb will apply to a plasma. Computing dielectric properties can be very difficult and require lots of attention to subtle details. Using one approach for a totally different system will not likely work or give grossly inaccurate results. One example would be the case of the dielectric boundary conditions, which is a very minor factor when looking at forces but a major factor for the total dipole fluctuations.
Is there any other way I can work around to calculate the dielectric constant for plasma from simulations?
The closest recent paper I could find after an exhaustive* search was Phys. Rev. E 103, 053203 (2021) - Simulations and experiments of phase separation in binary dusty plasmas . Have you read it or tried anything similar?
*ten minutes. But to be fair, that’s a lot of femtoseconds!
Thank you for your efforts. I have read a few papers on phase separation earlier, however, I couldn’t find much help from them.