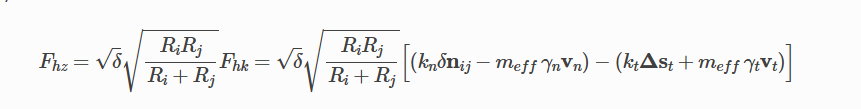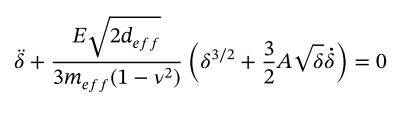I have created a two-atom model to test the collision time and restitution coefficient between particles and used the following parameters:
- Particle diameter: 0.0001 m
- Particle density: 2500 kg/m³
- Contact style:
pair_style granular
- Contact parameters:
pair_coeff * * hertz kn gamma_n tangential linear_history kt gamma_t 0
Where:
kn = 37e9
kt = 45e9
gamman = 95468
gammat = 47734
For the simulation, I fixed one atom and applied an initial velocity of 10 m/s to the other atom:
velocity nve_group set 0 0 10
From the simulation results, the collision time is 2.8e-7s, and the restitution coefficient (post-collision velocity/initial velocity) is 1.
However, after performing an integration using the following equation (derived from the Hertz contact model):
y1, y2 = y
dydt = [y2, -E * np.sqrt(2 * deff) / (3 * meff * (1 - v0**2)) * (y1**(3/2) + 3/2 * A * np.sqrt(y1) * y2)]
where y1 is displacement and y2 is velocity, I calculated the collision time to be 2.3e-07s and the restitution coefficient to be 0.5.
for the granular simulation, I only get an approximate restitution coefficient of 0.5 after scaling the Damping Coefficient by a factor of 30,000,000.
Can anyone help me identify what might be wrong in my calculations or if there is a misunderstanding of the concepts involved?
The input file and the result file
#! bin/bash
# file header
atom_style sphere
atom_modify map array
dimension 3
boundary p p f
newton off
comm_modify vel yes
units si
region reg block 0 0.001 0 0.001 -0.0001 0.0005 units box
create_box 1 reg
neighbor 0.0001 bin
neigh_modify every 1 delay 0
pair_style gran/hertz/history 36630036630.03663 45248868778.28054 95468.99737449684 47734.49868724842 0.5 1
pair_coeff * *
create_atoms 1 single 0.0 0.0 0.0004
create_atoms 1 single 0.0 0.0 0.0001
group fixed id 1
group nve_group id 2
velocity fixed zero linear
velocity fixed zero angular
velocity nve_group set 0 0 10
timestep 2.3430273328382426e-09
set group all diameter 0.0001 density 2500
fix integr nve_group nve/sphere
compute 1 nve_group com
fix brlc nve_group aveforce NULL NULL NULL
thermo_style custom step atoms f_brlc[3] c_1[3]
thermo 17
thermo_modify lost ignore norm no
shell mkdir post
shell mkdir restart
variable m_time equal time
variable m_atoms equal atoms
fix ave_data all ave/time 1 10 10 v_m_time f_brlc[3] c_1[3] file plate.txt title1 "" title2 "step time nf y"
dump dmp all cfg 1707 post/dump*.cfg mass type xs ys zs id type x y z vx vy vz fx fy fz radius
run 1
run 17071 upto
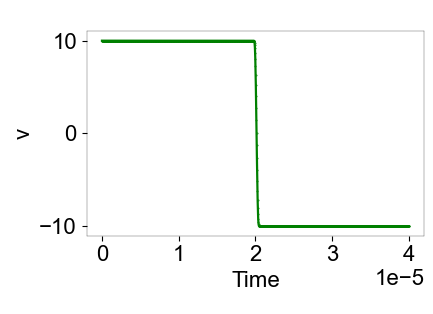
is attached.
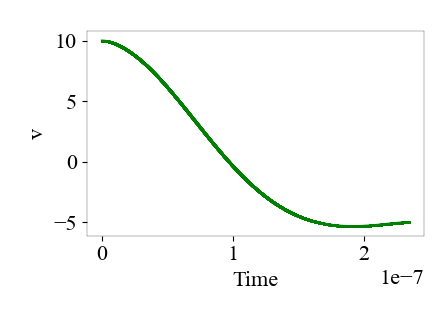
I can’t comment on what might be wrong with your equation (nor am I quite sure what the variables in it are), but I’ll point out that your input script is actually using pair gran/hertz/history not pair granular. Are you sure it’s applying the damping forces you expect it to (viscoelastic vs. mass_velocity)?
Pair granular also now has a coeff_restitution damping option which lets you specify the coefficient of restitution using a Tsuji form of damping forces. Maybe this might be more helpful?
Thank you for your reminder. It made me re-examine my model, and I found that I had some misunderstandings about certain parameters in my model: the second parameter of linear_history should be the multiplier for the normal damping. However, the issue still persists. In fact, the two definitions I am using are equivalent:
pair_style granular
pair_coeff * * hertz {kn} {gamman} tangential linear_history {kt} 0.5 0.5
by default damping = viscoelastic
And the Hertz model, where gammat = 0.5 * gamman
pair_style gran/hertz/history {kn} {kt} {gamman} {gammat} 0.5 1
pair_coeff * *
According to the documentation, they correspond to the following equation,
According to the above equation, I saw the following integral equation in the paper to calculate the collision time and recovery coefficient
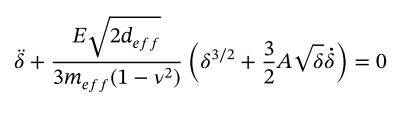
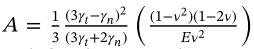
My expectation is that the results calculated by LAMMPS should be consistent with the results I compute using the equations.
But as mentioned above, when I take the following parameters:
kn kt gamma_n gamma_t
36630036630 45248868778 95468 47734
The calculated result of the equation is e=0.5, while the simulated result is e=1.0
What is the paper you are referring to?
Your expression looks similar (but maybe not exact) to Eq. 18 in Brilliantov et al. 1996 so I’m guessing you mean that paper. If so, why do you set his viscous constants \eta_{1/2} equal to the LAMMPS damping constants \gamma_{n/t}?
If it’s purely normal contact, wouldn’t the dynamics be independent of \gamma_t?
Thank you for the reminder. It is indeed an issue with the integral equation. This is equation (12) from the paper 10.1029/2019JB019016, but it uses the same symbols, gamma_n and gamma_t, as the contact force equations (8) and (9), which has indeed caused confusion.
I noticed that the coeff_restitution model you mentioned allows specifying the restitution coefficient, and I have also tested this model. I found that it achieves the same restitution coefficient at different speeds, but the measured restitution coefficient is usually higher than the specified one. Is this normal?
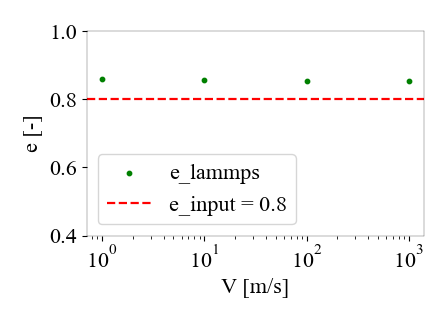
For the paper you cited, you might try contacting the authors to figure out variables.
For the coeff_restitution model, you might be getting a small shift because you’re only integrating one particle’s position which could affect dynamics. Namely, one particle effectively has infinite mass which is not accounted for in the calculation of the damping coefficient. There is an example script included in LAMMPS, examples/granular/in.restitution, which might be helpful to compare to.