Constraining a dummy atom

LAMMPS LAMMPS Development
1

Hello :slight_smile:

I need to make an MD simulation for a compound whose molecules contemplate a virtual site within the scope of the force field I need to use. Given atoms i, j, k lying in the end of my molecule (black circles in the figure below), the idea is that the virtual site (grey circle) should be, at each time step, (i) at a fixed distance d from atom i, (ii) at a fixed angle theta, which is formed by the vector r_ij and the vector going from atom i to the virtual site (this angle is also indicated in the figure), and (iii) in the same plane as atoms i, j and k.

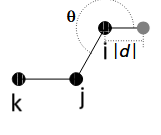
figure

I am here trying to figure out how/if I can make this work with the fix rattle/shake - for sure the fix rigid will not work. It is very straightforward to fix the distance d and angle theta, but I am not seeing any way I would, on top of that, be able to fix something else to indirectly keep the virtual site in the same plane as the atoms i, j, k in the rightful way (e.g. unless I am geometrically blind at the moment, I think I could accomplish that by additionally fixing the angle formed between atom i, the virtual site and atom k, but then this is not quite what I want, since this angle should be able to vary while the virtual site is still on the plane of atoms i, j and k). Does anyone know any LAMMPS command available that would allow me to accomplish this? Just the link to the page or names of the commands would already help tons!

Thanks!
Cecilia

EDIT: forgot to say that I am not a fan of setting up harmonic dihedral potentials with huge force constants in this particular case (although I can keep the constraints just fine, I will take a unfeasible long time to equilibrate the system in my experience).

2

I don’t think that fix rattle/shake can work. They require that you can do regular time stepping first, but that is impossible with a massless virtual site and assigning a reasonable mass would mess up your dynamics.

Fix rigid could work, if you are willing to also have the distance between atom i and j at a fixed length. Then you only need to assign a tiny nonzero mass (say 1.0e-100) to the to bypass the test for zero masses.

Beyond that, things are looking bleak without considering to program a custom time integration fix that will update the position of the dummy particle as needed.

3

Oh, I had not foreseen this :"D

Maybe then the fix rigid is the best compromise since I don’t know how to code in c++ and, even if I knew, don’t think i would trust myself to go modify source codes for something of this magnitude (seems complex).

It should be criminal to develop force fields with dummy atoms + 57194891 constraints :"D

Many thanks for the help!