Dear Lammps Users,
I am trying to choose the optimum Coulomb cutoff and K-Space accuracy for my system.
I am working on a minimized 331 super cell Tobermorite structure with 2520 atoms. The smallest dimension for the triclinic cell is 18.6 A. I am using a core-shell model and a flexible SPC water model to represent my system, which were used extensively in representing clay structures in literature.
Most of the studies i found in literature were using a K-Space accuracy around 10^-6 and 10^-8 for solving the long range coulombic interactions using Lammps. However, i find that as i change the coulomb cutoff, the total coulombic energy (ecoul+elong) changes for the same K-Space Accuracy. I understand that changing the cutoff is not supposed to change the energy value since using coul/long is supposed to calculate it up to infinity.
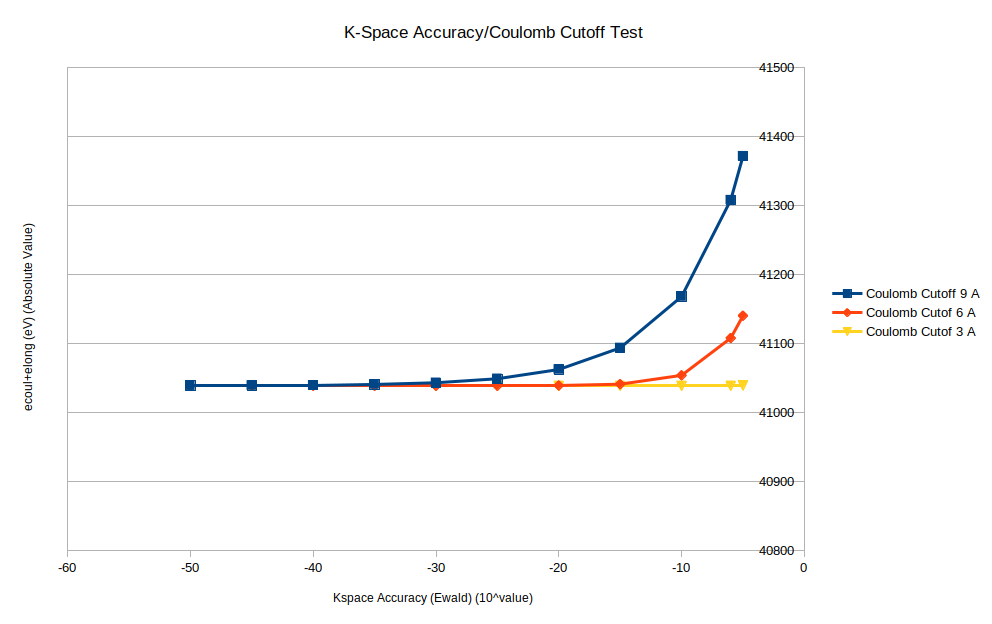
I have attached a graph for a convergence study i have done. In this study, i have varied the K-Space accuracy from 10^-50 to 10^-5 with an increment of 5 for the coulomb cutoff 9A, 6A and 3A. (The energy values on the y-axis represents the absolute values for the sum of the ecoul and elong.
As the graph shows, i need to go to a very high accuracy values or very small coulomb cutoff so that i can have a reliable and converging energy values, which i find very suspicious.
The structure i am working on is stable, minimized and was tested on GULP and gave the same value of the converged energy in Lammps.
At 9A coulomb cutoff, convergence in gulp was a lot faster (required smaller K-Space accuracy).
what might cause such a behavior? Thank you in advance.
Best regards
Ahmed
Dear Lammps Users,
I am trying to choose the optimum Coulomb cutoff and K-Space accuracy for my system.
I am working on a minimized 331 super cell Tobermorite structure with 2520 atoms. The smallest dimension for the triclinic cell is 18.6 A. I am using a core-shell model and a flexible SPC water model to represent my system, which were used extensively in representing clay structures in literature.
Most of the studies i found in literature were using a K-Space accuracy around 10^-6 and 10^-8 for solving the long range coulombic interactions using Lammps. However, i find that as i change the coulomb cutoff, the total coulombic energy (ecoul+elong) changes for the same K-Space Accuracy. I understand that changing the cutoff is not supposed to change the energy value since using coul/long is supposed to calculate it up to infinity.
with the default setting in LAMMPS of using 12-bit tabulation for coulomb interactions, there is no gain in accuracy possible by choosing a kspace convergence smaller than 1e-5. please also note, that forces converge much faster than energies in this case and energies are just a diagnostic, not anything that affects the trajectory.
also, turning off tabulation will not help much. i expect you can look at kspace convergence until up to 1e-8, since the error function complement is not computed by using the math library function (about 2-3x slower and not fully portable anyway) but by using an approximation that is only consistent with single precision floating point accuracy.
I have attached a graph for a convergence study i have done. In this study, i have varied the K-Space accuracy from 10^-50 to 10^-5 with an increment of 5 for the coulomb cutoff 9A, 6A and 3A. (The energy values on the y-axis represents the absolute values for the sum of the ecoul and elong.
As the graph shows, i need to go to a very high accuracy values or very small coulomb cutoff so that i can have a reliable and converging energy values, which i find very suspicious.
looking for energy convergence is pointless in this case. what matters are forces, and also the perceived accuracy is not what you have for the reasons outlined above. there is work pending (for several years now) that can lift the real space coulomb precision to double precision without loss of performance, but there are some technical limitations (and time availability constraints) that have kept us from following this through.
axel.
Dear Axel,
Thank you for your reply. I agree that absolute energies are not meaningful. However, energy differences are important!
My question to Lammps developers is there a way, in current Lammps version, to enforce faster convergence for coulomb energy with respect to precision at any cutoff for the real space?
Another question to all Lammps community, are there any molecular dynamics studies that used a low real space cutoff (as small as 3 A)?
Best regards
Ahmed
Dear Axel,
Thank you for your reply. I agree that absolute energies are not meaningful. However, energy differences are important!
that is what i was saying (look at the forces!), but that was not what you were discussing and the more important point i made was that you were looking at inconsistent settings where you were trying to achieve a precision that is impossible to achieve due to limitations of the real space computation. thus all of those numbers are essentially bogus and thus meaningless.
My question to Lammps developers is there a way, in current Lammps version, to enforce faster convergence for coulomb energy with respect to precision at any cutoff for the real space?
you are missing my point. i have nothing to add to what i stated this far.
Another question to all Lammps community, are there any molecular dynamics studies that used a low real space cutoff (as small as 3 A)?
a 3\AA cutoff makes limited sense. however, if you do choose such short cutoffs, you also need to consider the long-range effects of the lennard-jones r**6 terms, as it is done in the pppm/disp and ewald/disp kspace styles. please look up the corresponding publications for a discussion of accuracy of those.
axel.
also, what tells you that the convergence parameter in LAMMPS and GULP are comparable?
if you want to compare, you have to use the exact same cutoffs in real-space and k-space as the estimators for accuracy may be based on different heuristics.
axel.
Dear Axel,
Thank you for your prompt reply,
Regarding gulp comparison, i made sure that all the parameters are exactly the same and was confirmed for many structures and simulations.
Regarding the cutoff, i am varying only coulomb real space cutoff while all other interactions have cutoff of 9 angstroms. On the other hand, are you aware of any studies that have used such a small cutoff for real space coulomb energy while maintaining a reasonable cutoff for the rest of the potentials?
Regards
Ahmed
Dear Axel,
Thank you for your prompt reply,
Regarding gulp comparison, i made sure that all the parameters are exactly the same and was confirmed for many structures and simulations.
sorry, but people have claimed lots of things in the past and that they had checked everything and made no mistakes, and then there were still grave inconsistencies when looking at the details. so i won’t take your say-so on it.
Regarding the cutoff, i am varying only coulomb real space cutoff while all other interactions have cutoff of 9 angstroms. On the other hand, are you aware of any studies that have used such a small cutoff for real space coulomb energy while maintaining a reasonable cutoff for the rest of the potentials?
i consider 9\AA rather aggressive for LJ interactions (12-14\AA is more in sync with common practice).
also, there is little value in choosing a shorter coulomb cutoff than the LJ cutoff, as that will only increase the time spent on kspace without significantly reducing the cost of the real space computation (which is dominated by the computing of the distance of pairs of particles.
that is, unless you also shorten the LJ cutoff and that requires a long-range treatment of the LJ r**6 term as well.
i already pointed you to references that you should look up and study. i have a strong distaste for people not paying attention and needlessly repeating questions that was already responded to. i am done commenting on this topic now.
axel.
