Deviation from equipartition theorem in small system

LAMMPS LAMMPS Beginners
1

Hi everyone！
I’m trying to simulate a small system with two particles interacting by harmonic potential of a spring, and use the NVT intergrator for the simulation. And the version of Lammps is 20 Nov. 2019.
However, as I processed my data, I found that the potential energy of this system disagree with what epuipartition theorem told us it should be(i.e. 3kT/2), instead its value slightly deviates from 3kT/2.
Is this because the system is too small?

Here are some results :
1.the energy distribution for a system above with kT=120,dt=0.005,tau=0.5.the dashlines are the average values of kinetic(yellow) and potential(cyan) energy.
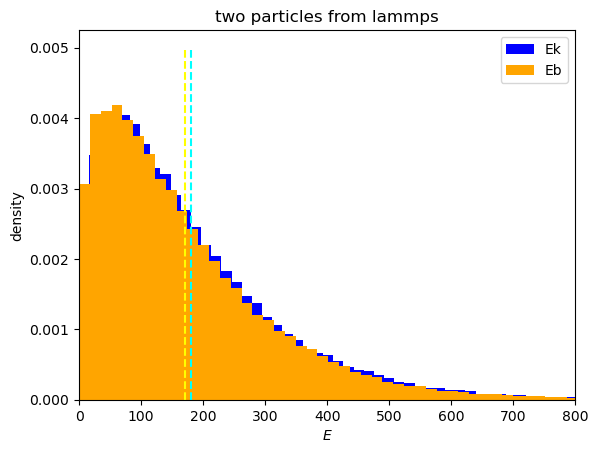
couple
2.then I change the temperature and calculate their average potential energy

1145
11451250×64 71.7 KB

and my .in file and .data file are as follows:
1.in file

#1.Initialize
clear 
units lj
atom_style molecular

boundary f f f 
read_data coupledog.data 

#2. potential 
bond_style harmonic
bond_coeff 1 0.5 1.0

#4. data
thermo 100
thermo_style custom step temp ke ebond etotal 
thermo_modify norm no


#5.run
timestep 0.005
fix 10 all nvt temp 120.0 120.0 0.5

run 10000000
  1. data file
LAMMPS data file for couple


2 atoms
1 bonds

1 atom types
1 bond types

-5000.0  5000.0  xlo  xhi
-5000.0  5000.0  ylo  yhi
-5000.0  5000.0  zlo  zhi

Masses

1 1.0

Atoms

1    1    1    -0.014430    3.483336    5.619503
2   1   1    0.000000    0.000000    0.000000

Bonds

1   1   1    2

Best regards,
Mark

2

Your simulation input deck does not allow for equilibration, i.e. you start with zero kinetic energy but there is no indication that you compute your averages only after the system has reached equilibrium. This would explain a bias toward a lower kinetic energy average.

Please also note that if you want to compare accuracy for runs with different temperature, you need to adjust the timestep and the Nose-Hoover coupling via the time constant (best by choosing the time constant as a multiple of the timestep) to have comparable accuracy in time integration and thermostat coupling (you want the Nose-Hoover thermostat only to couple weakly to your system).

4

Heartfelt Thanks to you， akohlmey!
I’ve figured it out, your reply makes a difference. This deviation of potential energy is because the the length of spring of harmonic potential is set to 1.0, rather than zero. when i set it to zero, all the diviation disappears.
But it still cofuses me that why the finite length of spring results in a coninuous deviation from Gibbs ditribution(instead of a discontinuous one ).Maybe you know the reason?
In addition, there’s a question left. The ‘fix nvt’ command in lammps followed by a keyword ‘Tdamp’ ,which is related to the Q, thermotat mass, in the referances, is there an equation shows the relation between Tdamp and Q?