Hi, I’m working on analyzing trajectory RDF(Radial Distribution Function).
I tried two tools, lammps rdf output and MDAnalysis for RDF.
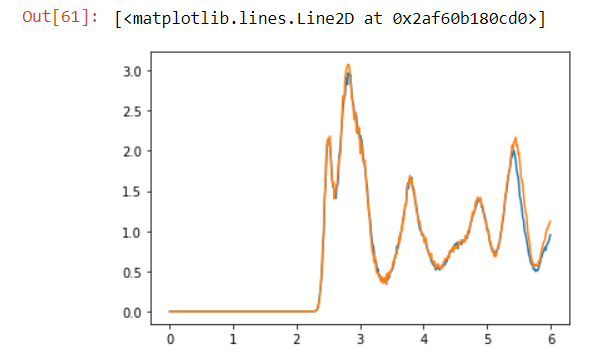
Here will be a comparision for two tools. Both are under Rcutoff=6.0, and nbins=500, steps=10 ,I comfirm.
It is obvious that there is a shift. How to explain that? I believe MDAnalysis will calculate the “mic” distance under PBC (capped_distance function if you are interested). Besides, such a shift seems to happen when the R exceed half the box minimum. (~ 5.1 armstrong)
So, does lammps RDF analysis consider PBC distance condition? I m a green hand in cpp, i guess someone who familiar with the code can help me?
feel sorry if I m wrong about LAMMPS, haha. 
blue for MDA, yellow for LAMMPS
Minimum image conventions do not apply to LAMMPS. Periodic boundary conditions are implemented as an extension to the domain decomposition scheme that LAMMPS uses. There each MPI process “owns” local atoms that are within its subdomain and in addition maintains “ghost” atoms that are copies from neighboring subdomains. Because of that, LAMMPS can in principle handle cutoffs larger than half the box (at the cost of more communication and additional storage). The g(r) code uses the standard neighbor list for pair interactions and thus operates similar to pair styles. Cases where minimum image conventions are still required do so because of additional details of the specific feature.
I cannot speak for MDAnalysis (you need to ask its developers), but I know about the g(r) implementation in VMD. This one applies minimum image conventions, but can compute the g(r) up to sqrt(0.5)*box by adjusting the normalization function. Because the the normalization volume is shrinking with growing r beyond 0.5*box the error of those values is growing.
1 Like
Many thanks for your generous explanation.
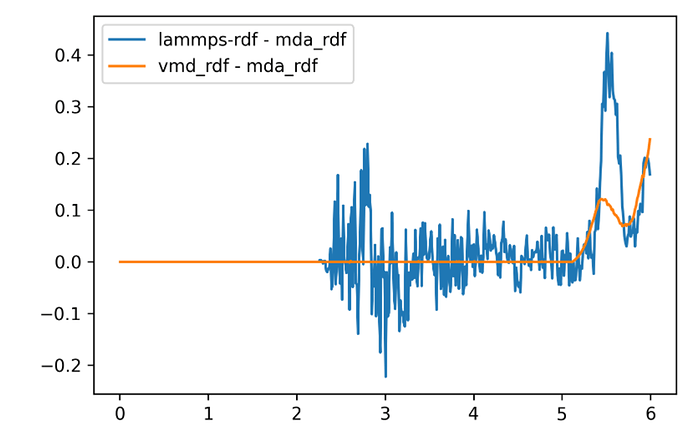
Now I tried 3 rdf tools( lammps-output, mda-rdf, vmd-rdf)
There are the difference of such 3 methods.
It seems that MDA and VMD result are consistent within a meaningful range (which I mean ~5.05 in my box), and shows different when out of 5.05 armstrong. I guess it is the “shrinking volume” you explained? There must be diffrent around VMD and MDA.
Also, the error of LAMMPS seems to be non-negligible.
It is impossible to discuss this without having sufficient information about what you are computing and plotting and how exactly you generated that data. You could be comparing rather different data, e.g. not averaging the same way.
1 Like
![]()