I am a new user of pymatgen, and have been working on elastic tensor calculations. Some of my calculations have been coming out rather strange (it seems like the symmetry_reduce function is catching symmetries that aren’t actually symmetries), and so I went searching for the workflow that is normally used with pymatgen. I found atomate workflow, but I was looking for something that I could compare my code to, and not a workflow creator. Is there anything like this?
Can you elaborate a bit on what you’re looking for? The atomate elastic workflow constructor generates all of the structures and stores them with the appropriate VASP parameters, what is your code doing?
Also, if you’ve encountered a bug or unexpected behavior in symmetry_reduce, we’d love to try to fix it in pymatgen. Can you help us reproduce your issue there?
Yes, sorry for my ambiguity. I will share the relevant portion of my python file if it is helpful, but I am creating a DeformedStructureSet object after relaxing the structure if VASP. From there, I pass the deformations member data into the symmetry_reduce function and have just been analyzing which deformations have symmetry to other deformations. More accurately, I am actually looking at the structures that come from these deformations. I compared them with a symmetry_reduce called on Tensor(deformed_structures.lattice.matrix) and got different results, so I’m just a bit confused.
This investigation all started because we noticed that the strains and stresses for c44 when plotting were symmetric about y=-x, which did not make sense because a negative stress like that should be close, but not exactly the same as the positive. It should be noted that I am by no means an expert in materials science, and in fact I am just a beginner, so it is quite possible that I messed something up. Also, if anything I said didn’t make sense, feel free to ask me for clarification.
from pymatgen import Structure
from pymatgen.symmetry.analyzer import SpacegroupAnalyzer
from pymatgen.io.vasp.outputs import Vasprun
from pymatgen.io.vasp.inputs import Poscar
from pymatgen.analysis.elasticity.strain import DeformedStructureSet, Strain
from pymatgen.analysis.elasticity.stress import Stress
from pymatgen.analysis.elasticity.elastic import ElasticTensor
from pymatgen.core.tensors import symmetry_reduce, Tensor
from numpy import arange, array
import os
from multiprocessing import Process, Pool
from itertools import product
def second():
# Retrieve the relaxed structure
vasprun=Vasprun('vasprun.xml',parse_potcar_file=False)
relaxed_struct=vasprun.ionic_steps[-1]['structure']
# Get all calculations necessary for elastic constant calculations
deformed_struct_set=DeformedStructureSet(relaxed_struct)
deformed_structs=deformed_struct_set.deformed_structures
deformations=deformed_struct_set.deformations
# We need to change these into Tensor objects so that the symmetry_reduce function will work
deformed_structs_lattice=[Tensor(struct.lattice.matrix) for struct in deformed_struct_set.deformed_structures]
# Get the symmetry dictionary and the structure dictionary
sym_struct_dict=symmetry_reduce(deformed_structs_lattice,relaxed_struct)
sym_deform_dict=symmetry_reduce(deformations,relaxed_struct)
struct_dict={}
deform_dict={}
for i in range(len(deformed_structs)):
struct_dict[deformed_structs_lattice[i]]=deformed_structs[i]
deform_dict[deformations[i]]=deformed_structs[i]
symm_reduced_structs=list(sym_struct_dict.keys())
for i in range(len(symm_reduced_structs)):
print()
print()
print()
print()
print('start structure symmetry')
# This is the structure that we start with.
print(symm_reduced_structs[i].zeroed())
for symm in sym_struct_dict[symm_reduced_structs[i]]:
print('symmetry struct')
# This structure is a symmetry
print(symm_reduced_structs[i].transform(symm).zeroed())
print("break")
symm_reduced_deforms=list(sym_deform_dict.keys())
for i in range(len(symm_reduced_deforms)):
print()
print()
print()
print()
print('start deform symmetry')
# This is the structure that corresponds to the deformation that we start with
print(symm_reduced_deforms[i].zeroed())
for symm in sym_deform_dict[symm_reduced_deforms[i]]:
print('symmetry deform')
# This is the structure that corresponds to the deformation that is a symmetry
print(symm_reduced_deforms[i].transform(symm).zeroed())
second()
1 Like
I’m not sure about this, but I don’t think symmetry_reducing the list of lattices should work, because lattices can look different under different applied strains that are symmetrically equivalent. For example, consider a 1x2x3 supercell of a conventional fcc lattice. Any of the 90 degree rotations about a given axis will render an equivalent structure, but the lattice will not be.
I think you should just symmetry reduce on strain/deformation, which is what we do in the workflow constructor for atomate, and then apply those deformations to the structure.
Ok, interesting. I will have to think about that a little bit more. I can’t really see it in my mind yet. Possibly, you can be of help with the line of thinking that led us down this line of investigation (hopefully I can explain it well enough). Our first try through creating elastic constants, we passed in the deformations to the symmetry_reduce as you said, then evaluated the vasp calculations from the POSCARs created by the structures relating to these deformations. After this, we read in the stresses and transform them as well as the strains according to the proper symmetry. After we are done, we took a look at the data that is used for the fit (these are the istrains and istresses in the from_independent_strains function). We noticed on the c44 strains and stresses that these were exactly symmetric about y=-x. We thought that they would be close, but exactly the same all the way down to 8 or 10 significant figures, so they are from the same VASP calculations. Do you know why this might be?
Yes, +/- shear strains should be equivalent for certain symmetries, right? What’s the structure you’re deforming?
It is fcc, so it does have a high level of symmetry. I just didn’t think that shear strains would be symmetric. Maybe this could be cleared up with a question. When we introduce a strain, is the proper picture something like this?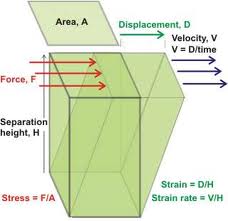 
I was imagining it more pushing on one corner in the (1,1,1) direction.
Yep, I think this is correct, so you can imagine when you push in the opposite direction, for e.g. fcc the resultant deformed structures will be related by an 180 degree rotation of the system (or a reflection about the axis perpendicular to the shear deformation). I see why it’s confusing though, intuitively it seems like it should be the same as the case of compressive/tensile strain.
As an aside, keep in mind that pymatgen’s symmetry (via spglib) finding is subject to tolerances, so if the symmetry is close, but not exact, you might have issues with symmetry reduction. Also to a certain extent doing the calculation in both direction might smooth out minor numerical issues, but generally we’ve found that it doesn’t make much of a difference, especially since we re-fit the output tensor to the original structure’s symmetry anyway.
Awesome, thanks a ton for your help. I really appreciate it.