Energy-Volume minimum of water does not match zero pressure

[shmattoso]

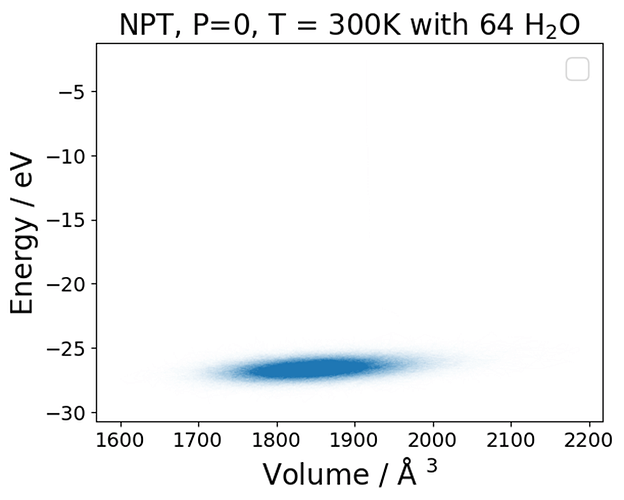
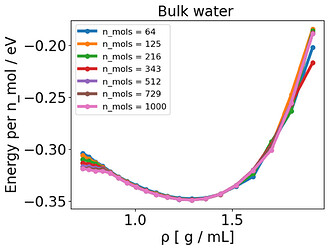
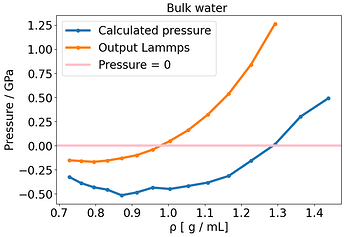
I have been running bulk NVT TIP3P simulations of 64 water molecules where I vary the cell size and keep the number of water molecules constant, giving me different densities and an energy-volume or energy-density curve.

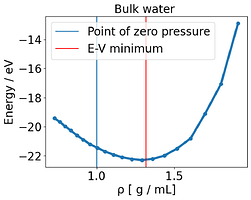
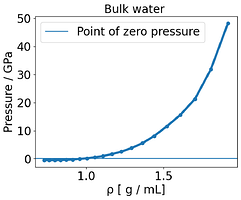
I noticed some inconsistent behavior, where essentially the E-V minimum, located around 1.3 g /mL, does not match of the point where the pressure is zero (around 1.0 g /mL) . There is a mismatch between energy and pressure.

In order to sort this out, I tried out a wide range of possibilities, such as investigating the thermostat (Langevin x CSVR), time constant , time step (0.1-1.0 fs), simulation time (up to 20 ns), number of molecules (up to 1000), pppm cutoff (down to 10^-10 ), coulomb cutoff (10-20 Å ), lammps version, shake x rattle, shake or rattle cutoff (down to 10^-10 ), increased H -mass (1-16 g), using harmonic bonds instead of fixed bonds and tail corrections.

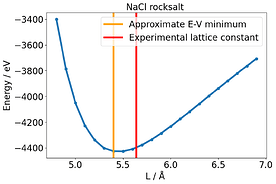
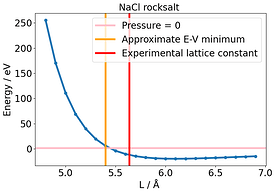
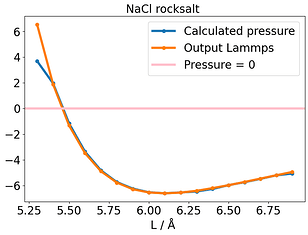
None could solve this E-V mismatch. To compare this with another system, I used NaCl rocksalt and varied the lattice constant. Here there is no discrepancy and the E-V minimum corresponds to where P= 0 .

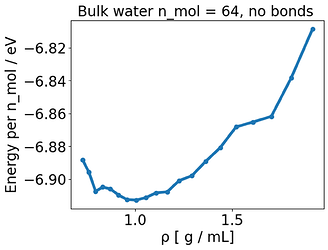
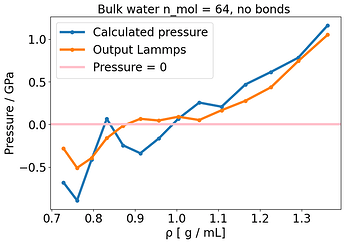
What made the E-V minimum correspond to where P= 0 for water, was completely removing any kind of bonded interaction, so this behavior is connected to the presence of the bonds, somehow. Of course if I remove the bonds I don’t have a reasonable water model anymore but it suggests that this issue is somehow related to the bonds.

My questions therefore are:

• Is this E-V pressure mismatch inherent to TIP3P or similar bonded-water models? If not, how could I attempt solve it?
• The context of this is that I will add an ion to water in order to calculate a solvation energy. I want to do this by having E_{\text{ion_H2O}} - E_{\text{bulk_H2O}}, both cases at zero pressure. So for this I needed the proper energy at zero pressure, a.k.a the E-V minimum which currently is inconsistent. Since I will use an energy difference in the end, maybe the E-V pressure mismatch is not so relevant?

The version I used was 2021.10.27, however I tried with 2023.08.02 as well and didn’t see any difference.

I attach an example file of a simulation with Rattle.
control.inp (675 Bytes)
structure.inp (11.0 KB)
potential.inp (428 Bytes)

[Germain]

Hi @shmattoso,

TIPnP models, especially TIP3P, and SPCE have numerous thermodynamical anomalies not only compared to experiment but also compared to expected behavior of water model. Water is actually hard to get right in classical simulation, and is often parametrized to give correct results as a solvent and close to ambient conditions.

Jorgensen and his group extensively published on the subject so you might look into their work. Fortunately as you also recalled, it is energy fluctuations and differences that are important in thermodynamic computations so you should be good, see here for example.

I qualitatively reproduced your results out of curiosity, so I think you are correct in your computation, but am curious when you say:

@shmattoso

What made the E-V minimum correspond to where P= 0 for water, was completely removing any kind of bonded interaction, so this behavior is connected to the presence of the bonds, somehow. Of course if I remove the bonds I don’t have a reasonable water model anymore but it suggests that this issue is somehow related to the bonds.

Did you remove the bonds entirely? Because rigid bonds and angles are already at equilibrium and do not contribute to the pressure with style zero. However water molecules geometry is indeed important for water properties and TIP3P is known to get it wrong in the solid phase (ice phases are unstable and melt way to fast). I mention this also because water is not very compressible and the very high increase of the pressure makes me think there is some glassy transition happening at some point here but I didn’t check MSD or had a look to the system as I did this with a quick and dirty training script.

I am also curious to see how TIP4P behaves so I am trying to make the same simulations to compare the values.

[shmattoso]

Hi @Germain, thank you very much for your input and help. Indeed this seems to be intrinsic to TIP3P and ok for my current endeavors, hopefully.

It is great you were able to reproduce my results. About the bonds, when I say I removed bonds, I really mean completely removing any kind of bond/angle definition in the structure file and also in the potential file, so there is no trace of bonds whatsoever. Indeed the pressure is not the problem since it is zero around the density of 1.0 g / mL, as it should be. The energy that seems inconsistent with the pressure.

I didn’t do any further structural analysis of these higher density simulations, I can just see visually some phase transitions that may take nanoseconds to form. This is however not super relevant to my point, in my opinion, because even if something ‘‘strange’’ is happening at high densities >1.3 g /mL or so, shouldn’t we still see some kind of minimum at around 1.0 g /mL, where the pressure is zero?

Another test I did was to run a NPT simulation this time. Indeed the barostat gave me the correct approximate density of around 1.0 g / mL. However, if I plot the scatter of the energy with volume, I should see in principle some kind of parabolic minimum, but I see a slope, consistent with the NVT calculations from before.
I’m waiting curiously for your TIP4P results, let’s see what it shows. Thank you for the references as well.

[srtee]

The “mismatch” is due to the internal energy of the volume degrees of freedom that are held constant in NVT, but freed (and thermalized, with an associated heat capacity) in NPT.

That is: consider all configurations of SPC water in the 0 bar NPT ensemble. Over the Boltzmann distribution, the average water density will be (slightly less than) 1 g/cc.

But there is some subset of configurations with water density equal to 1.3g/cc. That subset of configurations is extremely underweighted relative to 1g/cc configurations because of both the higher internal pressure and the higher internal energy of the volume degrees of freedom.

But that latter energy contribution is not calculated by the internal pressure estimator (or else that estimator would only work in NPT, and not NVT).

Mathematically: over an NPT ensemble at set pressure P, the expectation value of internal pressure is

\langle P_{int} \rangle = P

but the expectation value of PV energy (since V fluctuates) is

\langle P_{int} V \rangle = P \langle V \rangle - k_B T

See: 5.2: Pressure and Work Virial Theorems - Chemistry LibreTexts

The anticorrelation is related to extra energy in the volume DoFs, and in turn to the difference between isochoric and isobaric heat capacities.

This “shows up” in your water simulations because, as your results show, water is relatively compressible on molecular length scales and therefore an energy contribution of a few eV (per system size) is measurable. The same offset exists in your NaCl systems, but is negligible against a pressure of several eVs per % bulk strain.

[Germain]

I also suspected that there was something about the computation of the enthalpy but didn’t know about this exact calculation, the fact that removing the rotational degrees of freedom reduced the discrepancy should have been a hint. TIP4P behaving the same way (with 1000 molecules) was another one.

I should go through Tuckerman’s class or book, I’m sure they contain some useful stuff on the ensembles I missed in the past.

[shmattoso]

Thank you for your reply.

Based on my understanding, this can’t be the reason for the discrepancy I observed. My reasoning is that while what you wrote is correct, this energy discrepancy would be order of 30 meV which is much less than what I observed in my E-V curves. Furthermore, this discrepancy would scale with 1/N as N increases. I ran calculations then for different N’s and did not observe any difference. Additionally, when removing the bonds, as previously mentioned, the discrepancy ceases to exist.

I also investigated now if the calculated pressure -dE/dV matches the output of LAMMPS. As expected there is a discrepancy with water, however with NaCl it matches well.

Additionally, despite the rough curve, the pressures match well with non-bonded water.

[srtee]

Okay, fine, let’s actually make a proper thermodynamic calculation. With A being the Helmholtz free energy (which is the natural thermodynamic potential of an NVT system):

U = A + TS \\ \Rightarrow \frac{\partial U}{\partial V} = \frac{\partial A}{\partial V} + T \frac{\partial S}{\partial V} \\ \hspace{3.1em} = - P + T \frac{\partial P}{\partial T} \\ \hspace{9.5em} = - P + T \times \frac{1}{V} \frac{\partial V}{\partial T} \times V \frac{\partial P}{\partial V} \\ \hspace{4.1em} = - P - T \alpha_V K_0

We go from line 2 to line 3 using the Maxwell relation in double derivatives of A and in line 5 use the definitions of the (volumetric) coefficient of thermal expansion \alpha_V and the bulk modulus K_0.

See? Only the derivative of the microcanonical internal energy in volume is the pressure. By thermodynamic equivalence, the derivative of the Helmholtz free energy in the NVT ensemble is also the pressure, but the derivative of the canonical internal energy is not.

This explains your results very well. The sodium chloride crystal has very little difference in the region of zero bulk modulus (as your own graph shows, the pressure changes very little with lattice constant past 5.75 angstroms), and I would bet that the thermal expansion coefficient of the purely Coulombic sodium chloride severely underestimates experimentally obtainable values.

On the other hand, SPC/E water has a thermal expansion coefficient of about 600 ppm/K at 300 K (three times its experimental value – https://www.sciencedirect.com/science/article/pii/S0378381224000955), so T \alpha_V is about 18%, and multiplied by a bulk modulus of about 2.1 GPa this gives an offset of about 0.36 GPa – which is very near what you got at 1.0 g/mL.

[Germain]

@shmattoso Also note that the results difference vanishes when removing the bonds because you go from a rigid molecular model to a LJ+Coulomb fluid which is closer to your salt model and has not much to do with rigid water model anymore. The elastic moduli in this case must be way lower than water.

This explains that.