I am trying to replicate the DPD simulation in LAMMPS. With that, I mean the simulation leading up to Figure 1 in the paper cited in all the LAMMPS DPD documentations: Groot and Warren, J Chem Phys, 107: 4423-4435 (1997). DOI: 10.1063/1.474784.
Now, I can actually replicate the results they get, but only shape and tendency wise, the data I find is offset on the x-axis compared to the paper’s, and it is not clear to me, why this would be the case.
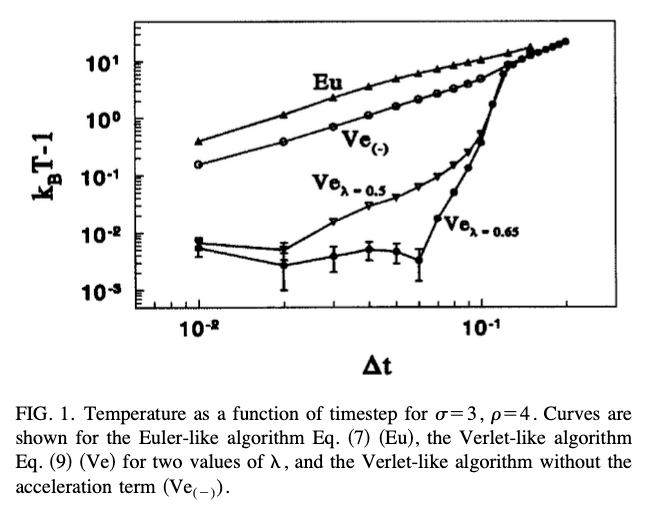
This is the plot I try to replicate:
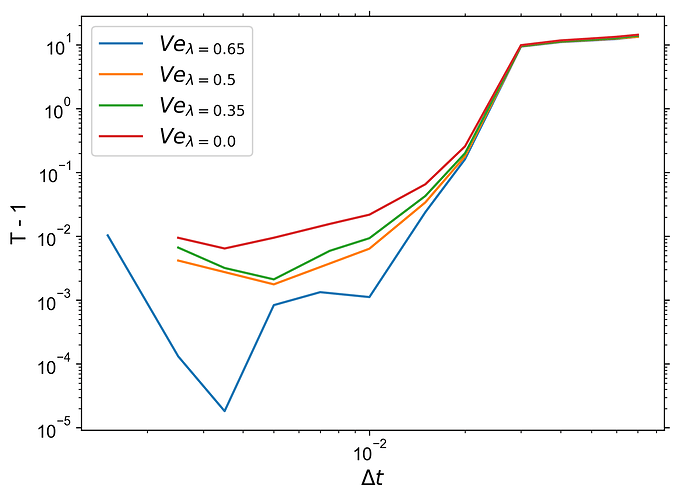
and this is how it currently looks like:
As you can see, the x-axis is very different.
My LAMMPS input looks like this (standalone, you should be able to run like this):
# LAMMPS input file: fig. 1 replica of Groot, Warren, 1997
units lj
atom_style tdpd 1
variable kb equal 1.0
comm_modify vel yes
variable seed equal 2570894
# create the box and atoms with rho = 4
region thebox block 0 10 0 10 0 10
create_box 2 thebox
create_atoms 1 random 4000 ${seed} thebox
mass * 1
variable sigma equal 3
variable T equal 1.
variable gamma equal 0.5*${sigma}*${sigma}/(${kb}*${T})
variable A equal 25
variable cutoff equal 1.0
pair_style dpd ${T} ${cutoff} ${seed}
pair_coeff * * ${A} ${gamma} ${cutoff}
fix 1 all mvv/tdpd 1.0
# run_style verlet
run 100
# output we are interested in
compute 3 all temp/com
thermo_style custom step temp dt press c_3 vol
thermo 1
# dump 1 all custom 1000 ./output/fig-1.dump.txt id fx fy fz
# actual simulation
variable timeStp index 0.0015 0.0025 0.0035 0.005 0.007 0.01 0.015 0.02 0.0025 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14 0.15 0.2 0.25 # it will loose atoms at some point, but we don't care
label loop0
# adjust the time-step
timestep ${timeStp}
# re-run the simulation with the new time-step
run 20000
next timeStp
jump SELF loop0
and my LAMMPS version is LAMMPS (23 Jun 2022), as installed on MacOS using Homebrew.
I would expect to be able to use LAMMPS in accordance with the documentation to reproduce said paper, but it is possible that I am misunderstanding something.
Some observations:
- I require much more than the 200 steps Groot & Warren report having done to get a stable result. This would hint, that either they did not have a stable result, or the random forces I get are too strong.
- I would consider the general behaviour to be reproduced, ignoring the offset on the x-axis.
I would kindly ask for some feedback on what could be reasons for this replication to fail, or if anyone notices any issues in the code, I would like to understand why my simulations break down at a different time-step.