Dear LAMMPS users,
I am currently trying to calculate the free energy difference on silver clusters.
Charge of the cluster is the only parameter being perturbed, this is to be used as the criteria for reduction of the cluster. All silver atoms are +1 charge and equilibrated using qeq with ethlyene glycol (EG) as the solvent.
I calculated the FEP of each cluster (post-process using rerun) at particular time step (i.e. 50,000 step), by repeating the FEP calculation with different lambda. Interaction between silver atoms and EG was “switched off” by using neighbor_modify exclude command.
The following command where used:
compute cluster 1 cluster/atom 2.9
compute cc2 1 chunk/atom c_cluster compress yes
compute size 1 property/chunk cc2 count
fix 2 1 ave/histo 2000 1 2000 0 30 30 c_size mode vector ave one beyond ignore file 1t1_nvt.histo
dump clu 1 custom {freq_frame2} {lmp_data}_chunk.cltr c_cc2 id
variable agg1 atom “c_cc2==1”
variable agg2 atom “c_cc2==2”
group c1 dynamic 1 var agg1 every 2000
group c2 dynamic 1 var agg2 every 2000
variable dlambda equal 0.1 #(varied from 0.1-1.0)
variable ag equal 1.0*v_dlambda
compute cFEP c1 fep 433 atom charge 1 v_ag volume no
compute cFEP1 c2 fep 433 atom charge 1 v_ag volume no
fix fFEP c1 ave/time 1 1 2000 c_cFEP[1] c_cFEP[2] file bar01.lmp
fix fFEP1 c2 ave/time 1 1 2000 c_cFEP1[1] c_cFEP1[2] file bar02.lmp
group-id = 1 -> silver atoms
However, the FEP calculated on one of the clusters shows the following trend (other clusters show the same trend):
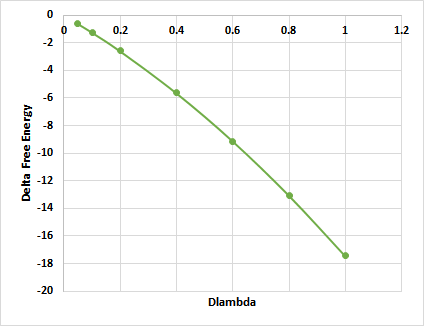
Since all the FEP calculated are negative value even when the lambda = 1, there is no optimum charge can be deduced.
I have tried to study some journals related to FEP calculation, but so far I haven’t found FEP calculation with charge perturbation only. Any comments and suggestions are welcome.
Thank you.
The way you are doing it, you are changing the charges of the clusters between 0 and their original charge. Based on your data, it appears their original charge is the optimum. If this is somehow not what you expected, then either what you are doing is not actually what you are doing or your expectation is not correct. I can imagine that if your cluster is charge-stabilized, i.e., U_{charged} < 0, then the “ideal” configuration would be to have charges of infinite size, and hence there is no local optimum in the charge. If that is not the case, read on.
A basic and therefore stupid question: You did run the simulations for different values of lambda right? I found the literature to be quite decent when I dealt with it, I cited the following two articles because I applied Bennett’s acceptance ratio but I remember the Mezei papers to be quite good too:
Zwanzig R W. J. Chem. Phys., 22:(1954) 1420–1426.
Bennett C H. J. Comput. Phys., 22:(1976) 245–268.
As for your point of perturbing charge vs. perturbing potential energy:
Typically the potential energy is perturbed, but you can think of a charge perturbation as a potential energy perturbation if you rewrite your potential energy as:
U_{total} = U_{non-charged} + U_{charged} and then rewrite U_{charged} as
U_{charged} = \sum_{i=1}^N\sum_{j=(i+1}}^N q_i q_j (other stuff) -->
U_{charged}(\lambda) = \sum_{i=1}^N\sum_{j=(i+1}}^N (\lambda q_i) (\lambda q_j) (other stuff) = \lambda^2 \sum_{i=1}^N\sum_{j=(i+1}}^N q_i q_j (other stuff)
= \lambda^2 U_{charged}(\lambda = 1}
So in essence you are applying the perturbation
U_{total}(\lambda) = U_{non-charged} + \lambda^2 U_{charged}.

Thank you for your insightful comments and suggestions.
I’ll study the papers which you suggested and try to re-approach the problem.
Some clarification, yes I did run the FEP calculation on different lambda from 0.1 to 1.0.

