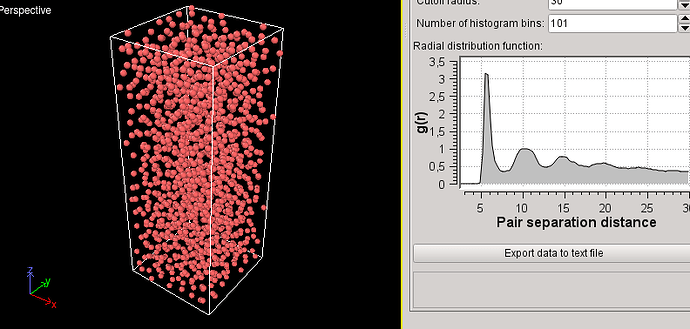
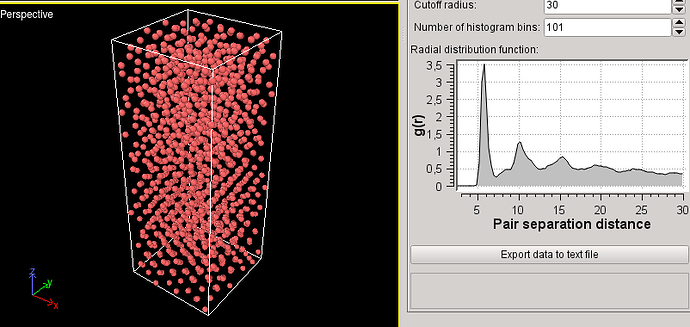
Dear all,
I am using lammps version 20160725-14.
I am using a corse-grained model of PMMA where each particle represents a monomer (attached my restart file “pmma.restart”). It is the amorphous result of:
1-) Creation of fcc crystal of particles
2-) Minimization
3-) Equilibration in NVT at 300 K
3-) Heating up to 1000 K
4-) Equilibration in NVT at 1000 K
5-) Cooling down to 300 K
6-) Equilibration in npt using (300 K and 10 bar)
My ultimate goal is to use it as a matrix for gold deposition. Experimentally I have long times between depositions (1 s) and I am interested in investigating both the details of growth of nanoparticles and also percolation as the dose increases.
So, I started to use fix tfmc to perform uniform-acceptance force-bias Monte Carlo (fbMC). Of course I know that it will not reach 1 s, but I think some prolongation can be enough. I read the papers and I am still testing it with PMMA alone to see how it works. I have tested several values of Delta (maximum displacement length), inclusing 0.10 (that authors suggested for most of materials). Despite 0.5 seems a too large value, I have used too, as it is 10% of the nearest neighbor distance for my system.
But the negative potential energy increases and I lose the amorphous structure.
Attached also my code (PMMA_MC.in).
Any help will be very welcome!
Dr. Fernanda S Teixeira
Laboratory of Thin Films
Institute of Physics - University of Sao Paulo
PMMA_MC.in (1.54 KB)
pmma.restart (113 KB)
2017-04-27 17:33 GMT+02:00 Fernanda S Teixeira <[email protected]...>:
Dear all,
I am using lammps version 20160725-14.
I am using a corse-grained model of PMMA where each particle represents a
monomer (attached my restart file “pmma.restart”). It is the amorphous
result of:
1-) Creation of fcc crystal of particles
2-) Minimization
3-) Equilibration in NVT at 300 K
3-) Heating up to 1000 K
4-) Equilibration in NVT at 1000 K
5-) Cooling down to 300 K
6-) Equilibration in npt using (300 K and 10 bar)
My ultimate goal is to use it as a matrix for gold deposition.
Experimentally I have long times between depositions (1 s) and I am
interested in investigating both the details of growth of nanoparticles and
also percolation as the dose increases.
So, I started to use fix tfmc to perform uniform-acceptance force-bias
Monte Carlo (fbMC). Of course I know that it will not reach 1 s, but I
think some prolongation can be enough. I read the papers and I am still
testing it with PMMA alone to see how it works. I have tested several
values of Delta (maximum displacement length), inclusing 0.10 (that authors
suggested for most of materials). Despite 0.5 seems a too large value, I
have used too, as it is 10% of the nearest neighbor distance for my system.
But the negative potential energy increases and I lose the amorphous
structure.
What do you mean with "losing" the structure? Do you get lost atoms, or
does the structure change? An increasing potential energy is normal for
fbMC, and as long as you get no real spikes in the energy it should be OK.
I do know, though, that Lennard-Jones solids tend to be more sensitive to
the choice of the DELTA parameter, and since LJ is what you're using here
that might be related.
Kristof
The structure changes.
From this:
To that:
And I would like to keep the amorphous structure.
Fernanda
2017-04-27 21:37 GMT+02:00 Fernanda S Teixeira <[email protected]...>:
The structure changes.
From this:
To that:
And I would like to keep the amorphous structure.
If you minimize both, is the more ordered structure lower in energy? If so,
you can't really blame fbMC for producing it.
Kristof
Dear LAMMPS users,
I am getting confused: I get an error saying "Compute used in variable between runs is not current " although I have tried the tricks I found in the manual on the variable page. can anyone suggest what I am missing?
compute 3 all temp
run 0
variable b equal c_3
fix 2 all langevin 2.0 0.0 $b 278111 ###Langevin integrator Tstart Tstop 1/friction rndseed
thermo_style custom step temp enthalpy c_3 $b
run 100
I tried the command switch and the simulation hangs:
lammps-daily -v b -in input.lam
I am not sure what is going on or how to fix that.
With best wishes and many thanks in advance
Anna
Dear LAMMPS users,
I am getting confused: I get an error saying "Compute used in variable
between runs is not current " although I have tried the tricks I found
in the manual on the variable page. can anyone suggest what I am missing?
compute 3 all temp
run 0
variable b equal c_3
fix 2 all langevin 2.0 0.0 $b 278111 ###Langevin integrator
Tstart Tstop 1/friction rndseed
why so complicated? why use compute temp, when you can simply use the
"temp" thermo keyword. not even a variable is needed:
fix 2 all langevin 2.0 0.0 $(temp) 278111
but then again, what sense doe this command make? using the current
temperature as the thermostat relaxation time???
thermo_style custom step temp enthalpy c_3 $b
this is wrong, too. $b is immediate expansion -> will print a number ->
error due to unknown thermo keyword. you want v_b
but that would be pointless, as you can also use "temp" to get the same
result.
do you want something like this:
run 0
variable b equal $(temp)
thermo_style custom step temp enthalpy v_b
axel.
Thank you Axel,
That solved my problem, many thanks! it seems like I was overthinking. I have noticed in my earlier work that in diffusion (of an ensemble of 50 particles), for instance, to match with theoretical predictions, one has to always adjust the Langevin damping parameter to the temperature (if temperature is 2 and damping 1, the curve resulting from simulations will not match the prediction of the analytical Langevin solution for that given temperature), and because I am changing the temperature as a function of time, I believe this would be the reasonable thing to do for my system.
With best wishes
Anna
Thank you Axel,
That solved my problem, many thanks! it seems like I was overthinking. I
have noticed in my earlier work that in diffusion (of an ensemble of 50
particles), for instance, to match with theoretical predictions, one has to
always adjust the Langevin damping parameter to the temperature (if
temperature is 2 and damping 1, the curve resulting from simulations will
not match the prediction of the analytical Langevin solution for that given
temperature), and because I am changing the temperature as a function of
time, I believe this would be the reasonable thing to do for my system.
sorry, but this explanation doesn't make any sense to me. also, your
command doesn't change the thermostat time constant dynamically anyway.
axel.
Thank you Axel,
That solved my problem, many thanks! it seems like I was overthinking. I
have noticed in my earlier work that in diffusion (of an ensemble of 50
particles), for instance, to match with theoretical predictions, one has to
always adjust the Langevin damping parameter to the temperature (if
temperature is 2 and damping 1, the curve resulting from simulations will
not match the prediction of the analytical Langevin solution for that given
temperature), and because I am changing the temperature as a function of
time, I believe this would be the reasonable thing to do for my system.
sorry, but this explanation doesn't make any sense to me. also, your
command doesn't change the thermostat time constant dynamically anyway.
the only way, that i can see where you would have some kind of correlation
between the temperature and the relaxation time is a model, where you are
using fix langevin to represent a (simple) implicit solvent model. then the
relaxation time (or rather the damping constant) would be correlated to the
viscosity of your implicit solvent, which in turn could be correlated to
the temperature. ...and it may - by chance - work out for you when using
reduced units. but for example, when you have metal and real units, you
have the same unit for temperature (kelvin), but different time units. so
your claim of setting the relaxation time cannot work in this case.
axel.
Dear Axel,
Yes, the first case you mention (the implicit solvent) system that I work with, indeed, and with LJ units… I looked at temperature dependence some 4 years ago, and it was clear to me that for a Brownian (NVE+LJ) system one can only recover the analytical form of Langevin when T_damp=T, I never went deeper into trying to understand why, but simply adjusted the damping coefficient accordingly to recover correct diffusive properties. I have not looked at other systems/units from the perspective of this particular problem, and this is not a bug, I believe it is just something system specific that one needs to be careful about.
With best wishes,
Anna
Hi,
Potential energy of -618 eV for the more ordered structure and -606 eV for the amorphous. I understand what you mean. But for about 100000 steps, it seems that the fbMC works well, but suddenly there is a great decrease in potential energy AND also in pressure! I am getting NEGATIVE values of pressure.
Fernanda
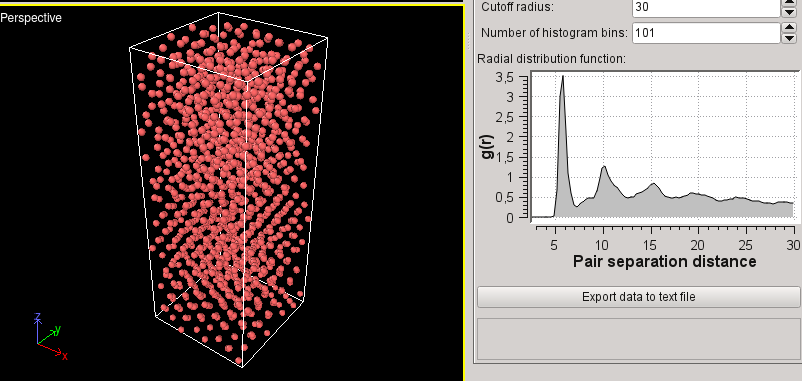
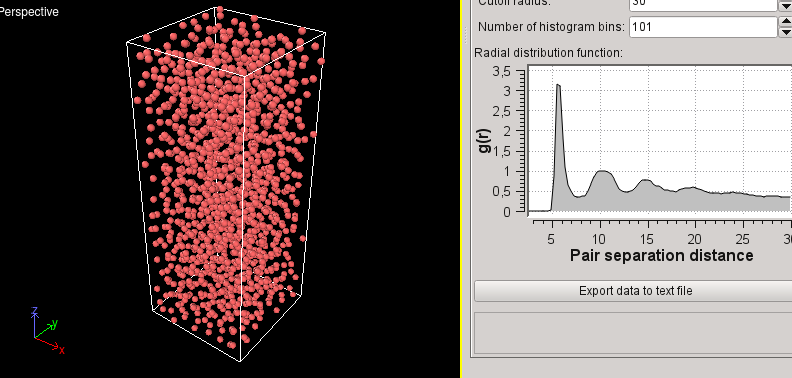
Hi,
Potential energy of -618 eV for the more ordered structure and -606 eV for
the amorphous. I understand what you mean. But for about 100000 steps, it
seems that the fbMC works well, but suddenly there is a great decrease in
potential energy AND also in pressure! I am getting NEGATIVE values of
pressure.
negative pressure is nothing to worry about. negative pressure just means,
that your system want to shrink.
what you are describing sounds like you have a phase transition happen.
your original configuration was in a metastable state and then managed to
drop into state of lower energy. on the atomic scale phase transitions have
large hystereses and - as an activated process - can be delayed for long
time periods, when the barriers are high. but in your case, they don't seem
that high, and adding a monte carlo process to your overall simulation will
either have no impact or will make it more likely to cross barriers.
as kristof already hinted at, it looks like the system in your simulation
is simply following the physics of the model.
axel.
Hi,
Potential energy of -618 eV for the more ordered structure and -606 eV
for the amorphous. I understand what you mean. But for about 100000 steps,
it seems that the fbMC works well, but suddenly there is a great decrease
in potential energy AND also in pressure! I am getting NEGATIVE values of
pressure.
negative pressure is nothing to worry about. negative pressure just
means, that your system want to shrink.
what you are describing sounds like you have a phase transition happen.
your original configuration was in a metastable state and then managed to
drop into state of lower energy. on the atomic scale phase transitions have
large hystereses and - as an activated process - can be delayed for long
time periods, when the barriers are high. but in your case, they don't seem
that high, and adding a monte carlo process to your overall simulation will
either have no impact or will make it more likely to cross barriers.
as kristof already hinted at, it looks like the system in your simulation
is simply following the physics of the model.
Yes. Essentially, fbMC is working exactly as advertised. The most
successful application of the method has been accelerating the formation of
(more) crystalline structures from amorphous starting configurations.
Kristof
Dear Axel and Kristof
That's perfect! Thank you for these valuable insights.
Fernanda
Quoting Kristof Bal <[email protected]...>: