Dear all,
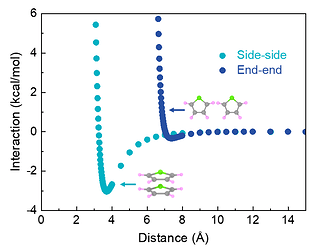
I am doing the fitting of gay-berne potential now, but I am not sure about the variables in the Gay-berne potential when fitting the energy-distance profile. I already have the end-to-end and face-to-face energy-distance profile of ring polymer, like the one below.
I have read many papers and noticed that they fit the energy-distance profile using GB potential that contains complex formulas and many variables, so I am not sure how to fit this energy-distance curve. In GB formulas, does sigma(ui,uj,rij) a variable? What about the ui,uj,rij? Do they need to fit?
I am sorry for making this question because it may not be the LAMMPS question, but I can not figure this out for a long time trial. I fitted this curve using 12-6 LJ potential before, which is simply because I only need to fit the sigma and epsilon in that function.
Best
Yang
You may find this topic relevant to understand the meaning of \sigma_{AB}(\omega_1,\omega_2,\vec{r}_{12}).
When you fit the Gay-Berne potential for specific orientations, the weighting coefficients change depending on the asymmetric overlap matrix, and they must be computed for any given direction of approach of two particles. To simplify the generation of the reference potentials, it was first suggested to use 12 orthogonal modes of approach in this seminal paper: “R. Berardi, C. Fava and C. Zannoni, Chem. Phys. Lett., 236, 462–468 (1995)”. However, the formulas for the 12 orthogonal configurations in that papers are misprinted. The correct ones are printed in a more recent paper of mine, Tables 2 to 4.
All you need to do is a multi-branch fit of two (or possibly all 12 orthogonal) potential energy curves simultaneously since they all depend on the same parameters \varepsilon_x, \varepsilon_y, \varepsilon_z, \sigma_x, \sigma_y, \sigma_z and \sigma_0.
Note that \varepsilon_0 is a scaling parameter used in the LAMMPS expression of the GB potential. After the fitting, just scale \varepsilon_x, \varepsilon_y, \varepsilon_z with respect to \varepsilon_0, e.g. max(\varepsilon_x, \varepsilon_y, \varepsilon_z).
I hope this helps.
Otello