GCMC with Electrode

[vishnu-kurupath]

GCMC with Electrode (conp)

Hi Everyone,
I have been trying to simulate GCMC adsorption of ions in a nanotube which act as metal-like walls. For the same I was trying to use both GCMC and the Electrode package in combination but with no success. Below I explain my procedure in detail. You can find my simulation files and lammps edits here.

1. Lammps Modifications

The primary focus of the lammps modifications was to repeoduce the energy calculations conducted by GCMC (FixGCMC::energy_full()) by obtaining the system state from inside the FixGCMC::energy_full() and running it as a new identical case but using nvt (only to compare the energy without changing the coordinates). For the same, the following changes are made to the lammps (2Aug2023_update2) source files (see the lammps folder here).

1.1 GCMC State

For getting the state of the system during the FixGCMC::energy_full() call, I add a output->write_dump() and output->write_restart call from inside the energy_full() function before it returns.

The original write_restart function (Output::write_restart) is modified such that it writes replaces the aestrik ‘*’ in filenames with the argument it receives (instead of the ntimestep). This is used in combination with a variable (energy_calls) to count the number of energy_full() was calls was used to get distinct restart files for each energy_full() calls.

This method was working very well for cases with Pure LJ and for LJ with P3M (1e-5 precision).

1.2 GCMC Energy

Apart from getting the system state, fix calls were added inside FixGCMC::energy_full() was changed such that it would resemble Verlet::run() with fix elecrode/conp. Table in the trials section lists all the additional modify functions that were added to the FixGCMC::energy_full() corresponding to a version index (s, se and senp).

• The s version corresponds to the original FixGCMC::energy_full().
• The se version includes all the functions from s and additionally modify functions that are part of the fix_electrode_conp mask (pre_exchange [modified, see below], post_neighbor, pre_reverse. pre_force exists in FixGCMC::ebergy_full() by default).
• The senp version has all the modify member calls as in the se version except for the modifed (see below) pre_exchange call.

Since, FixGCMC in itself is listed in the list_pre_exchange fix list, a modified pre_exchange_exclude function was added to modify.cpp (and modify.h) which accepts the id of the calling fix as an argument and executes all the fixes inside list_pre_exchange except the calling/invoking fix.

Lastly. utils::logmesg is used to print the energy from FixGCMC::energy_full() before the function returns.

2. Trials

I have used an LJ tube with a single charged particle as my initial system for simulation. The force field is a hybrid one combining mie/cut and coul/long. PBC is assumed along all the axes making the tube infinite along z.

I request you to find the rest of my simulation files in the 1.mie_pppm_electrode folder (shared previously).

Below is a table of energies that I obtain from the simulation based on my FixGCMC::energy_full() version corresponding to the function calls. The Y in table represnet presence of the modify call and N represent absence. The force_clear() in GCMC is implemented differently from that of verlet (and hence marked Y*). The energy provided for gcmc (second to last row) corresponds to the restart index 3 (elec_mc_3.restart in 1.mie_pppm_electrode folder/1.*.mc_* folders here).

modify calls	s	se	senp
post_int	N	N	N
pre_exchg	N	Y	N
comm_exchg	Y	Y	Y
pre_neigh	Y	Y	Y
post_neigh	N	Y	Y
frc_clr	Y*	Y*	Y*
pre_force	Y	Y	Y
pre_rev	N	Y	Y
comm_rev	N	Y	Y
post_force	Y	Y	Y
eof_step	N	N	N
energies	s	se	senp
gcmc	327333560.79	327337203.67	327337203.67
md_restart	148.807581	148.807581	148.807581

Note: Only the algo cg (1e-20) option of the electrode/conp works when used in combination with GCMC. Both the other algos (mat_inv and mat_cg) ends up giving me segmentation faults upon running.

There is large energy differences between the GCMC and the MD verlet here obtained from restart.
Also, the wall charges from the GCMC do not correspond to that obtained from MD when run from the restart.

Question

As mentioned, I would like to ensure that the electrode runs with GCMC reproducing energies consistent with a normal verlet run. It would be helpful if someone can throw some more insight into why I am not able to reproduce the energies properly. I can also share you any other data related to the case if needed.

EDIT-1 (13/4/24)

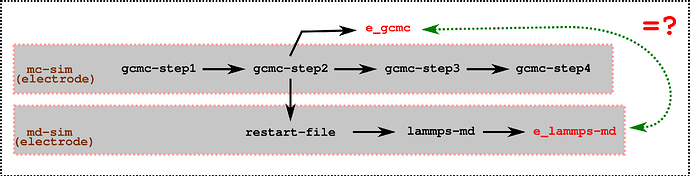
Below is an image for clarity !! I want to ensure (energy gcmc) e_gcmc = e_lammps-md

[srtee]

If you are using charge equilibration to change the charges on a carbon nanotube, wouldn’t the energy change?

[vishnu-kurupath]

If I have same set of atomic coordinates, charges and other settings for both the simulations, ideally I should get the same energy for both the simulations, ie., during GCMC and MD (NVT-frozen).

I have added an image in my original question for clarity !!

[srtee]

It is not that simple. I looked very briefly through your input scripts. I still do not fully understand what you are doing (especially since I have no experience with GCMC) but from the ELECTRODE point of view there are several major opportunities for disaster:

• You are using a dielectric. We have never officially tested that the code returns sensible results with such settings, because nobody else has used the code that way (because the community generally uses explicit solvents).

• You start the simulation with all wall atoms uncharged and only one cationic charge. Not only is this box non-neutral (more on that later), the PPPM accuracy will be much lower than estimated, because the total charge squared will be very small at initialisation but much larger once charges are induced. (Again, the community generally uses explicit solvents with significant charged particles so this usually isn’t an issue).

• I don’t see how your simulation can remain neutral. A conp fix with only one electrode at some potential will accumulate an arbitrary non-zero charge. A conq fix can keep the electrode at some specified charge, but when you try to insert a new ion, how will the electrode charge adjust to suit? A neutral simulation is important because the electrostatic energy of infinitely repeated non-neutral cells diverges.

This is in addition to any possible errors you may have picked up in your code modification.

[vishnu-kurupath]

Hi,

I assumed that the net charge that is induced on the wall (single electrode, symm off) from the presence of a charged particle would be equal and opposite to that of the charge on the inserted particle (similar to image charge method).

In short q_particle+sum(q_electrode/wall) = 0.0

Can you tell me why this is not so here. I did check the sum of charges in my system and as you mentioned they are not neutral.

Thank You
Vishnu

[srtee]

Without potential constraints (like in conq or in the “symmetrized” version of conp), the total charge induced on an electrode is simply what is required to set it “at potential” relative to zero at “infinity” – this only makes sense for a 2D periodic system where we can imagine a potential probe infinitely removed from the slab in some transverse direction. This is not guaranteed to neutralize the system – hence the need to introduce potential constraints that do enforce a stated total charge.

To be very clear, there is no general guarantee on induced charge electroneutrality even in classical continuum electrostatics. When a point charge Q is brought near a conducting surface at potential zero, the total charge on the surface can be integrated to -Q – but only integrated to infinity, with a convergence of 1/r, meaning that integrating a circle whose radius is ten times the height of the particle from the surface would still only contain 90% of the induced charge. A thought experiment with electrophoruses of difference sizes should confirm in your mind that in some limit it is the surface charge density, not the total charge, that is somehow matched – and in between there is some messy interpolative behaviour.

[vishnu-kurupath]

Hi,

I have switched from using conp to conq with a charge value (v_q) that is equal and opposite to the net charge from ions inside the electrode. Now I get a net charge for the system that is negligible \approx 10^{-15}. I have updated my new files in the 2.mie_pppm_electrode_conq folder in the drive folder I had shared.

However, I still find that there is manyfold difference in the energy between what is computed by the FixGCMC::energy_full() and what I am able to recover from the restart file. I provide the new energy values in the table below for the versions of LAMMPS I have compiled (as mentioned in my question).

modify calls	s	se	senp
post_int	N	N	N
pre_exchg	N	Y	N
comm_exchg	Y	Y	Y
pre_neigh	Y	Y	Y
post_neigh	N	Y	Y
frc_clr	Y*	Y*	Y*
pre_force	Y	Y	Y
pre_rev	N	Y	Y
comm_rev	N	Y	Y
post_force	Y	Y	Y
eof_step	N	N	N
energies	s	se	senp
gcmc	43.516	47.62	47.62
md_restart	-7.306	-7.306	-7.306

I am looking to tally the energy from MC and that of restarted MD to a reasonable precision (\approx 10^{-5} or 10^{-3}) so that I can be confident regarding my approach. Also, I suspect something wrong with my LAMMPS as both algo mat_inv and algo mat_cg throws up segmentation fault when implemented in my code.

Thanking You
Vishnu

[srtee]

Hi Vishnu,

I don’t know if you have addressed these other potentially simple but impactful issues:

@srtee

• You are using a dielectric. We have never officially tested that the code returns sensible results with such settings, because nobody else has used the code that way (because the community generally uses explicit solvents).
• You start the simulation with all wall atoms uncharged and only one cationic charge. Not only is this box non-neutral (more on that later), the PPPM accuracy will be much lower than estimated, because the total charge squared will be very small at initialisation but much larger once charges are induced. (Again, the community generally uses explicit solvents with significant charged particles so this usually isn’t an issue).

For the latter, you should experiment with using explicit kspace settings. That is, look through your logs for the run that has the highest kspace mesh numbers set, and exactly replicate the settings throughout all your calibration runs with something like

kspace_modify mesh 25 25 36 gewald 0.3

instead of letting LAMMPS try to estimate the mesh parameters on its own.

Please note that code modification and method development come with significant personal responsibility, and I do not have the availability right now to debug your code in full (nor, if I had the time or energy, would I probably have the expertise, since GCMC is a completely different area of molecular modelling that I have no experience in).