Hello Matsci community,
I al writing here since it is more a materials/algorithm than LAMMPS question, though related to LAMMPS and MD.
I am currently working on calculating the global pressure (similar to the pressure option in the LAMMPS thermo output) and stress tensor (specifically, the stress/atom tensor) using a LAMMPS dump file. I am not using the compute stress/atom from LAMMPS since the pair style I am using does not compute the stress/atom (RANN).
The dump file includes the following columns: ‘id’, ‘type’, ‘x’, ‘y’, ‘z’, ‘vx’, ‘vy’, ‘vz’, ‘fx’, ‘fy’, ‘fz’.
I started with computing the global pressure, as it is easier to compare with the pressure output in the LAMMPS log, but I’ve run into an issue. I’m using the virial stress definitions from the paper “General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions” and the LAMMPS documentation. The virial contribution I am using is: 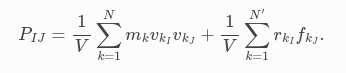 .
.
However, when I calculate the global pressure, the result is significantly lower than expected. For example, my system is equilibrated to 50 GPa (using Fe as a test case), but the calculated global pressure is around 2 GPa. I suspect I may be missing something important, either in terms of what can be computed from the dump file data, or there may be an arithmetic step I’m overlooking. Unfortunately, I believe this aspect isn’t discussed elsewhere?.
Bellow is a snippet of the code I am using:
# Conversion of columns so the pressure unit is GPa
df.x *=angstrom_to_meter
df.y *=angstrom_to_meter
df.z *=angstrom_to_meter
df.vx *=angstrom_ps_to_m_s
df.vy *=angstrom_ps_to_m_s
df.vz *=angstrom_ps_to_m_s
df.fx *= eV_to_J/angstrom_to_meter
df.fy *= eV_to_J/angstrom_to_meter
df.fz *= eV_to_J/angstrom_to_meter
#################### Calculations
# Kinetic energy tensor
velocities = df[['vx', 'vy', 'vz']].to_numpy()
kinetic_tensor = np.einsum('ij,ik->jk', velocities, velocities) * mass / volume
# Compute virial contribution
positions = df[['x', 'y', 'z']].to_numpy()
forces = df[['fx', 'fy', 'fz']].to_numpy()
virial_tensor = np.einsum('ij,ik->jk', positions, forces) / volume
# Total stress tensor
total_tensor = kinetic_tensor + virial_tensor
# Pressure (GPa)
pressure_gpa = -np.trace(total_tensor) / 3 / 1e9
# Print results
print("Kinetic Tensor (GPa):")
print(kinetic_tensor/ 1e9)
print("Virial Tensor (GPa):")
print(virial_tensor/ 1e9)
print("Total Tensor (GPa):")
print(total_tensor/ 1e9)
print("Pressure (GPa):", pressure_gpa)
If anyone has experience with this or can offer guidance on the correct procedure for calculating global pressure and stress/atom from LAMMPS dump, I would greatly appreciate your input.
Thank you in advance for any advice or suggestions!
Best regards,
Marco