Dear LAMMPS users,
I intend to exert a kind of force which will be attractive in the short range, and will be no interaction in the long range. Axel answered me in this mailing list several weeks ago, and he suggested me to use pair_style Python to customize the potential. This is a good idea but I will try it next step. The first step is, I finally understood that to some extent, I can directly use LJ potential.
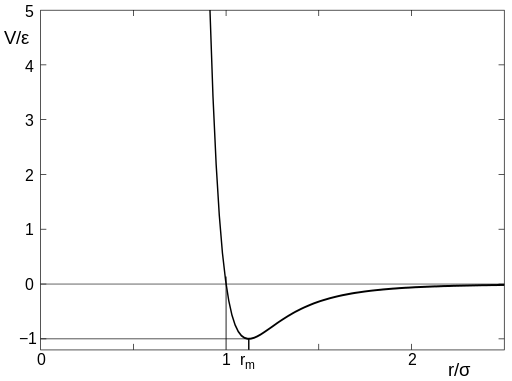
Based on Wikipedia, the x-axis reflects the distance between the centroid of two particles. I intend to let rm=d. d is the diameter of the particle in my system. In this sense, I think: 1. the particle will not overlap; 2. from just touch to the cutoff point, the interaction between two spheres will be the attraction; 3. after cutoff point, there will be not interaction. Are these assumptions correct? And I will let the particles be in Brownian motion.
So in LAMMPS, I choose lj unit, and about setting up diameter and par_coeff, what I wrote is
set type 1 diameter 1
set type 1 density 1
pair_style lj/cut 2.5
pair_coeff 1 1 10 0.89089871814
which means that I set epsilon=10.0, sigma=0.5^(1/6) because rm=2^(1/6)*sigma. But after running, I found that the interaction between particles is repulsive - once they are close enough (but not touch), they will kick away each other. I pasted my script at the end of this mail, and attached the .xyz file I dumped.
My question is that what the unit of length is in LJ unit system. More precisely, in the documentation, it said that distance=sigma, which looks like sigma is the unit of length. For example, when we set diameter to be 1, it is 1 sigma. But since we still need to set sigma in the pair_coeff command, it sounds like that sigma is not the unit of the length. Otherwise, when we set sigma = 0.89, it means that sigma = 0.89 sigma, which is confused.
#########################lj_test.txt##########################
variable x index 1
variable y index 1
variable z index 1
variable t index 100000
variable N index 80
units lj
timestep 0.00000001
atom_style sphere
boundary p p p
region A block 0 5 0 5 0 5
create_box 1 A
change_box all boundary p p p units box
create_atoms 1 random $N 22322 NULL
set type 1 diameter 1
set type 1 density 1
pair_style lj/cut 2.5
pair_coeff 1 1 10 0.89089871814
neighbor 1 bin
neigh_modify every 1 delay 1 check no
group one type 1
fix first_fix one langevin 1.0 1.0 100 12345
fix second_fix all nve
dump myDump1 one xyz 1000 lj_mpl_$N.xyz
run $t
lj_mpl_80.xyz (211 KB)