Hi @Germain,
Thanks, it is more clear now. But the force field still doesn’t work for my project. Here I want to describe my problem in a more detailed way. I guess there’s still sth wrong with how I enter the parameters.
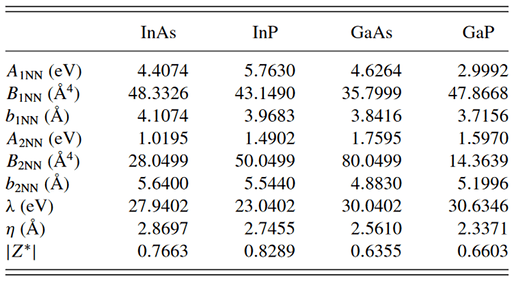
I want to use Stillinger-Weber + Coulomb force field to relax an InAs quantum dot. The origin force field fitted in paper is written in GULP format. Here’s the link for this paper: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.85.041306 and the origin file for GULP https://www.chemie.uni-hamburg.de/institute/pc/arbeitsgruppen/bester/downloads.html.
The form of this force field:
The potential proposed in this work consists of short-range two-body terms V_2(i,j), a three-body term V_3(i,j,k), and a long-range Coulomb term V_C(i,j).
\begin{aligned}V= & \sum_{i<j}^{j \in 1 N N} V_2(i, j)+\sum_{i<k}^{k \in 2 N N} V_2(i, k) +\sum_{i<j<k} V_3(i, j, k)+\sum_{i<j} V_C(i, j)\end{aligned}
The two body terms, which describe the short-range bond-stretching interactions between the first nearest neighbor (1NN) and second nearest neighbor (2NN) atoms, have the following form:
V_{2}(i,j)=\left\{ \begin{array}{l}A\left(\frac{B}{r_{ij}^{4}}-1\right)\exp\left(\frac{\rho}{r_{ij}-b}\right),r_{ij}<b\\0,r_{ij}\geqslant b\end{array}\right.
where r_{ij} denotes the distance between atom i and j , and b represents the cutoff distance of the interaction.
The three-body term corresponds to the contribution of an angle distortion with respect to the ideal tetrahedral angle and is given by:
V_3(i, j, k)=h\left(r_{i j}, r_{i k}\right)+h\left(r_{j i}, r_{j k}\right)+h\left(r_{k i}, r_{k j}\right)
where,
h\left(r_{i j}, r_{i k}\right)=\lambda \exp \left(\frac{\eta}{r_{i j}-b}+\frac{\eta}{r_{i k}-b}\right)\left(\cos \theta_{j i k}+\frac{1}{3}\right)^2
V_{C}(i,j)=\frac{Z_{i}^{*}Z_{j}^{*}}{\left|r_{ij}\right|}
The fitted parameters in paper:
\rho = 2.2819 for InAs read from GULP input.
Compared this with LAMMPS form:
\begin{aligned}
E & =\sum_i \sum_{j>i} \phi_2\left(r_{i j}\right)+\sum_i \sum_{j \neq i} \sum_{k>j} \phi_3\left(r_{i j}, r_{i k}, \theta_{i j k}\right) \\
\phi_2\left(r_{i j}\right) & =A_{i j} \epsilon_{i j}\left[B_{i j}\left(\frac{\sigma_{i j}}{r_{i j}}\right)^{p_{i j}}-\left(\frac{\sigma_{i j}}{r_{i j}}\right)^{q_{i j}}\right] \exp \left(\frac{\sigma_{i j}}{r_{i j}-a_{i j} \sigma_{i j}}\right) \\
\phi_3\left(r_{i j}, r_{i k}, \theta_{i j k}\right) & =\lambda_{i j k} \epsilon_{i j k}\left[\cos \theta_{i j k}-\cos \theta_{0 i j k}\right]^2 \exp \left(\frac{\gamma_{i j} \sigma_{i j}}{r_{i j}-a_{i j} \sigma_{i j}}\right) \exp \left(\frac{\gamma_{i k} \sigma_{i k}}{r_{i k}-a_{i k} \sigma_{i k}}\right)
\end{aligned}
We can get the parameter file for LAMMPS:
# Parameters for zincblende InAs from
# Table II of P. Han, G. Bester, PRB, 83, 174304 (2011)
#
# Note that there is a mistake in this reference (i.e. rho is
# missing in the definition of the potential and parameter table).
# The value for rho is found in the GULP input files at:
# https://www.chemie.uni-hamburg.de/institute/pc/arbeitsgruppen/bester/downloads.html
#
# All other parameters defined in the reference are correct.
#
# The twobody ik pair parameters are entered on the ikk line.
# The threebody ijk parameters (where i is the central atom)
# are defined on the ijk line.
#
# These entries are in LAMMPS "metal" units: epsilon = eV;
# sigma = Angstroms; other quantities are unitless
#
# for all interactions:
# eps = 1
# cos(theta) = -1/3
# p = 4
# q = 0
# other LAMMPS parameters are given in the reference as
# sigma = rho
# a = b / rho
# lambda = lambda
# gamma = eta / rho
# A = A
# B = B / rho^4
#
# eps sigma a lambda gamma cos(theta) A B p q tol
In In In 1.000000e+00 2.281900e+00 2.471625e+00 2.794020e+01 1.257592e+00 -3.333333e-01 1.019500e+00 1.034534e+00 4.000000e+00 0.000000e+00 0.000000e+00
As As As 1.000000e+00 2.281900e+00 2.471625e+00 2.794020e+01 1.257592e+00 -3.333333e-01 1.019500e+00 1.034534e+00 4.000000e+00 0.000000e+00 0.000000e+00
As In In 1.000000e+00 2.281900e+00 1.799991e+00 2.794020e+01 1.257592e+00 -3.333333e-01 4.407400e+00 1.782599e+00 4.000000e+00 0.000000e+00 0.000000e+00
In As As 1.000000e+00 2.281900e+00 1.799991e+00 2.794020e+01 1.257592e+00 -3.333333e-01 4.407400e+00 1.782599e+00 4.000000e+00 0.000000e+00 0.000000e+00
In In As 1.000000e+00 2.281900e+00 1.799991e+00 2.794020e+01 1.257592e+00 -3.333333e-01 4.407400e+00 1.782599e+00 4.000000e+00 0.000000e+00 0.000000e+00
In As In 1.000000e+00 2.281900e+00 2.471625e+00 2.794020e+01 1.257592e+00 -3.333333e-01 1.019500e+00 1.034534e+00 4.000000e+00 0.000000e+00 0.000000e+00
As In As 1.000000e+00 2.281900e+00 2.471625e+00 2.794020e+01 1.257592e+00 -3.333333e-01 1.019500e+00 1.034534e+00 4.000000e+00 0.000000e+00 0.000000e+00
As As In 1.000000e+00 2.281900e+00 1.799991e+00 2.794020e+01 1.257592e+00 -3.333333e-01 4.407400e+00 1.782599e+00 4.000000e+00 0.000000e+00 0.000000e+00
Is this correct? I think the problem may come from \epsilon and cutoff tol.
Is tol in LAMMPS defined by a \times \sigma ? (It is written in manual of LAMMPS, but the symbol is not clear…) And how do LAMMPS read different \epsilon_{ij} and \epsilon_{ijk}, since these two parameters are defined in the same line at the same place ?
Thanks,
Zui