Sorry @Tanmoy_Paul for the late reply. The issue of calculating formation energies correctly comes up very often, so I wanted to clear it up for anyone who stumbles upon this in the future:
When calculating formation energy by hand, you have to be extremely careful about energy normalization. When you have the energy result of a DFT calculation, there are three possible energy normalization schemes you could follow:
- Normalize the energy to a single atom (this is the standard eV/atom you see. In this framework, H2O effectively becomes H_{0.333}O_{0.666})
- Normalize the energy to a single formula unit (i.e. say your calculation of H2O contains 12 atoms → this would equal 4 formula units of H2O)
- Normalize the energy to the total number of atoms in the cell of the calculation (i.e., don’t divide the DFT output by anything)
When you write the equation for formation energy, you can choose to either do it with chemical potentials, which are already normalized by scheme #1, or with a reaction equation as has been done in this post (scheme #2). Just make sure that whatever method you pick has consistent normalization throughout. For the H2O example discussed here, this would be:
ΔE_f(H_2O) = E(H_2O) - E(H_2) - 0.5*E(O_2)
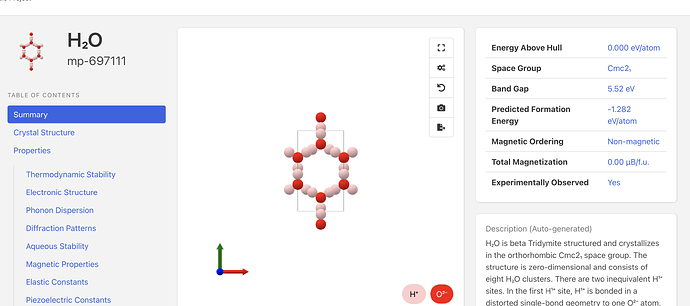
If you are using the Materials Project, you will get total energies for the entire calculation cells. The data below is from the new MP website and API:
- E(H2O) (12 atom cell) = -62.3132 eV → (divide by 4 to get -15.578 eV/f.u.)
- E(H2) (4 atom cell) = -13.5709 → (divide by 2 to get -6.78545 eV/f.u.)
- E(O2) (8 atom cell) = -39.5735 eV → (divide by 4 to get -9.893 eV/f.u.)
Then you plug in values:
ΔE_f(H2O) = -15.578 + 6.78545 + 0.5*9.896 = -3.845 eV/f.u.
Note that this is eV per formula unit. Finally, you can divide by the number of atoms in one formula unit (3 atoms per H2O) to get:
ΔE_f(H2O) = -3.845 eV/f.u. / 3 atoms = -1.282 eV/atom
This result exactly matches what is currently reported on the Materials Project site for mp-697111: