Dear OVITO Devolopers:
Recently, I am studying the twin-boundary of magnesium alloys. Previous studies show that atoms within the twin-boundary keep different atomistic strain state, i.e., extention or compression sites. Therefore, I want the quantity of local strain hydrostatic invariant to be calculated to character the atomic strain.
Through reading the third technical references of Li: von-mises shear strain invariant. I have made many trials, but failed all. Maybe the first-step of obtaining strain tensor was wrong.
First, I load a configuration fie (format: .cif) in OVITO, and no reference loded. Then, I begin to calculate the strain tensor. At last I used compute property to calculate the plane hydrostaic invariant by setting (StrainTensor.XX +StrainTensorYY)*0.5. But the results were totally wrong. Should I to redefine the d0 (obtained by equilbrium lattice) in the OVITO. Anyone can help me to calculate this quantity?
Taylor, Best wishes!
Dear Taylor,
I haven’t fully understood your workflow yet. Just to confirm, are you using the Atomic Strain Modifier? If so, what is your reference configuration?
Best,
Constanze
Hi, Constanze:
Yes, I used the Atomic Strain Modifier to operate it, and there have no reference configuration in operation. Because I read the basic theory of calculating local strain invariant by J.Li. The definition of the von-mises local strain invariant does’t need the reference configuration as below shows:
And in AtomEye (developed by J.Li), the Manual of illustrating calculate Atomistic Local von Mises Shear Strain Invariant also show no reference configuration to operate. And the screenshot of the Manual as below figure shows:
As Atomeye’s Manual show, the Atomeye output the local shear invariant, but what I need is the local hydrostatic invariant of the two-dimensional plane. Besides, the Least-Square Atomic Local Strain Tensor should provide the reference configuration.
Therefore my comprehension of processing the strain tensor to calculate the local strain invariant is just based on the current configuration. OVITO’s methods of obtaining strain tensor are almost based on the theory of J.Li.
Maybe my comprehension is wrong, but I don’t know where my fault.
Best wishes,
Taylor
Dear Taylor,
I should point out that OVITO cannot calculate reference-free strain tensor invariants like AtomEye does. In OVITO, there currently are two strain calculation functions:
-
The Atomic Strain modifier calculates local tensors (strain and deformation gradient) based on two input configurations: a reference and a deformed configuration. The calculation method is more or less identical to the one also known as “least-square atomic strain” found in AtomEye. Note that the Atomic Strain modifier in OVITO will automatically use the first frame of the loaded simulation trajectory as reference configuration if you do not explicitly specify some other configuration yourself.
-
The Elastic Strain Calculation modifier of OVITO works without an explicit atomic reference configuration. It implicitly uses a perfect, axis-aligned crystal lattice as reference to compute an atomic strain tensor. However, the calculation only works for atoms that are part of a defect-free region of the crystal, because only then can the atoms be mapped to the implicit reference lattice. For defect atoms, the method cannot compute a meaningful strain tensor. Thus, it is not suitable for calculating strain inside the atomistic core of a grain boundary.
Keep in mind that if you used the Atomic Strain modifier and did not specify a reference configuration, then OVITO was probably using the first frame of the simulation trajectory as reference. Perhaps this explains the unexpected calculation results you observed.
I am still trying to understand what property of the twin boundary you are interested in. Is the twin boundary aligned with the XY plane of the simulation coordinate system and would you like you compute the planar hydrostatic strain within that twin boundary plane? Do you expect an inhomogeneous strain distribution, and that’s why you would like to compute an atomically resolved strain measure?
Dear Constanze,
Thank you for answering me above questions, I have learned a lot from your explanations. Then, I am going to calculate the atomic local strain invariant by using the Atomeye. If can’t, maybe I will post for-help-email to J.L (developer of AtomEye).
To be honest, what I interest for atomistic strain of twin-boundary is just aim to copy a work of a famous paper titled Periodic Segregation of Solute Atoms in Fully Coherent Twin Boundaries (Science 340(6135):957-960). In this paper, the author found the solute atoms ordery decorate in the plane twin boundaries (TB) after the compressed samples go through heat treatment. The experimental HAADF-STEM images exhibit as below:
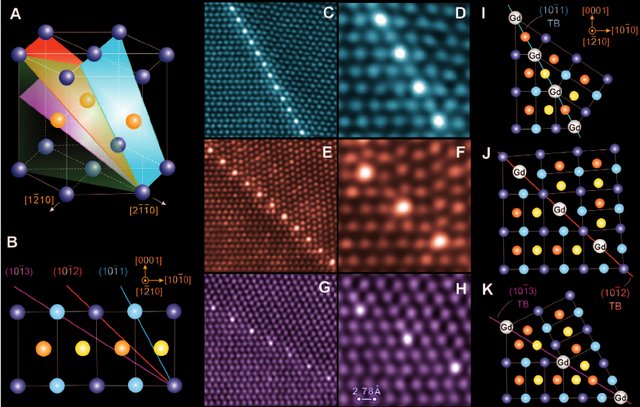
One can see that the atoms truly arranged on the TB plane with ordered arrangement. Then, the author, Professor Nie, want to explain this interesting phenomenon. Why solute atoms segregate into the TB plane with such ordered mode. Professor Nie and his colleagues firstly investigated the in-plane atomic atomic local strain hydrostatic invariant (ALSHI) in {10-11}, {10-12} and {10-13} twin boundaries of pure Mg. They calculated results are shown as below image:
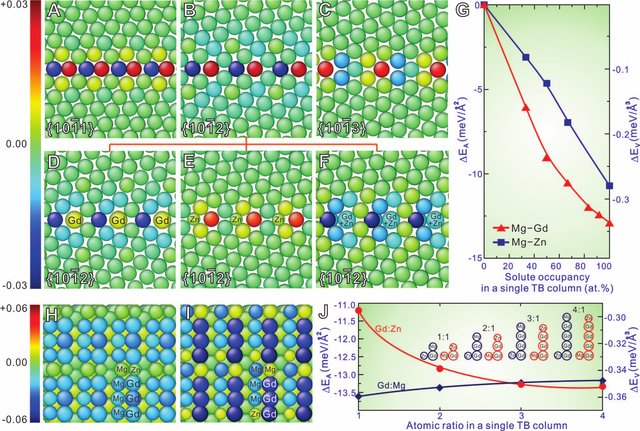
From image A to C, we can clearly obtain that the hydrostatic strain of atoms within TBs keep an ordered pattern, i.e., one extention strain (red balls in figure ) and one compression strain (dark blue balls in figure) occupied consecutively. Therefore, the solute atoms, Gd or Zn atoms in Mg-Gd-Zn alloys, occupy TBs orderly. Of course, they also calcuate other aspects to evaluate this phenomenon.
In the Supplementary Materials of this paper, they illustrated the methods to calculate atomic local strain invariants. A screenshot is also pasted as below:
May be what I understand is different from you, and a more clear idea may be came up after you read above materials.
Best wishes
Taylor.
Dear stukowski,
My research is also to study the twinning behaviour of Mg, and I wonder if I can use OVITO (Atomic strain ) to calculate the local shear strain along a specific twinning plane (not aligned with the box), for example the twining boundary(labeled in the diagram below using red dots and white line).
Regards,
Yuyang
Hi,
The Atomic Strain function of OVITO can compute the atomic deformation gradient tensor, which is a local quantity describing the full deformation in 3d space. Since this output is a tensor, you can project it onto any plane and extract shear components in your directions of interest.
I can’t give you more specific instructions right now, but I think the math operations required for this can be found in standard text books or on Wikipedia. You can perform the calculation either outside of OVITO (by hand), using OVITO’s Compute Property modifier, or a user-defined Python script modifier.
I assume that you already know the orientation of the twinning plane within the simulation coordinate system.



