Good day to everyone!
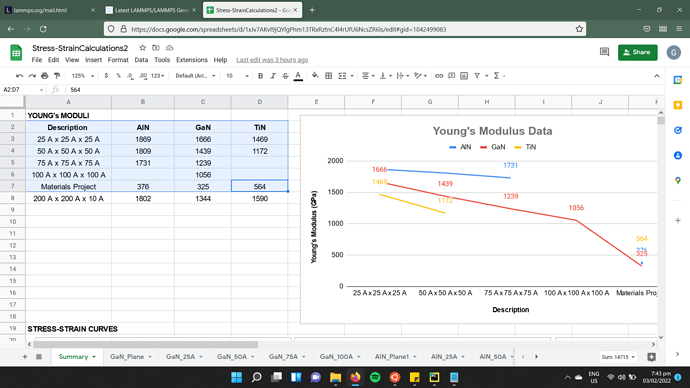
I’ve run multiple simulations where I stretch cubic models of AlN, GaN, and TiN along their x-axis at a constant strain rate. The initial runs yielded Young’s modulus values (taken as the slope of the generated stress-strain curves) that were way beyond experimental and theoretical values recorded in literature. As advised by my mentors, I ran further simulations that varied the size of the initial models to see if larger sizes would bring my results closer to known values. While it did, the results were still quite high (see screenshot attached).
Given all that, I wonder if there are ways to improve my results aside from increasing the model size (something that my laptop is poorly equipped to handle.) I’m considering varying the strain rate and initial system temperature after equilibration.
My input scripts generally follow this flow (following this LAMMPS tutorial: Uniaxial Tension - EVOCD):
------------------------ INITIALIZATION ----------------------------
units metal
atom_style atomic
dimension 3
boundary p p p
atom_modify map array
------------------------- SETTINGS ---------------------------------
variable a equal 3.00770274
variable b equal 3.00770274
variable c equal 3.00770274
#lattice hcp ${latconst}
region whole block 0 $a 0 $b 0 $c units lattice
create_box 2 whole
#create Ti atoms
lattice custom 1.0 &
a1 $a 0.0 0.0 &
a2 0.0 $b 0.0 &
a3 0.0 0.0 $c &
basis 0.50000000 0.50000000 0.50000000
create_atoms 1 region whole
#create N atoms
lattice custom 1.0 &
a1 $a 0.0 0.0 &
a2 0.0 $b 0.0 &
a3 0.0 0.0 $c &
basis 0.00000000 0.00000000 0.00000000
create_atoms 2 region whole
replicate 8 8 8
------------------------- POTENTIAL ---------------------------------
pair_style meam/c
pair_coeff * * libraryTiN.meam Ti N TiN.meam Ti N
neighbor 2.0 bin
neigh_modify delay 10 check yes
#-------------------------- COMPUTATIONS -------------------------------
compute csym all centro/atom fcc
compute peratom all pe/atom
------------------------- EQUILIBRATION ------------------------------------
reset_timestep 0
timestep 0.001
velocity all create 300 12345 mom yes rot no
fix 1 all npt temp 300 300 1 iso 0 0 1 drag 1
Set thermo output
thermo 10
thermo_style custom step lx ly lz press pxx pyy pzz pe temp
dump 1 all custom 10 equilibration_TiN.lammpstrj id type x y z ix iy iz c_peratom c_csym
write_data data.relaxationTiN
run 50000
unfix 1
undump 1
Store final cell length for strain calculations
variable tmp equal “lx”
variable L0 equal {tmp}
print "Initial Length, L0: {L0}"
------------------------- DEFORMATION ------------------------------------
reset_timestep 0
write_restart restart.TiN
fix 1 all npt temp 300 300 1 y 0 0 1 z 0 0 1 drag 1
variable srate equal 1.0e10
variable srate1 equal “v_srate / 1.0e12”
fix 2 all deform 1 x erate ${srate1} units box remap x
variable strain equal “(lx - v_L0)/v_L0”
variable p1 equal “v_strain”
variable p2 equal “-pxx/1000”
variable p3 equal “-pyy/1000”
variable p4 equal “-pzz/1000”
fix def1 all print 100 “{p1} {p2} {p3} {p4}” file TiN.deformation.txt screen no
thermo 10
thermo_style custom step v_strain temp v_p2 v_p3 v_p4 ke pe press
dump 1 all custom 10 deformation_TiN.lammpstrj id type x y z ix iy iz c_peratom c_csym
write_data data.deformationTiN
dump 2 all custom 10 data.atoms_deformation_TiN id type x y z ix iy iz
run 300000
Thank you very much for your time and patience!