Dear LAMMPS mailing list,
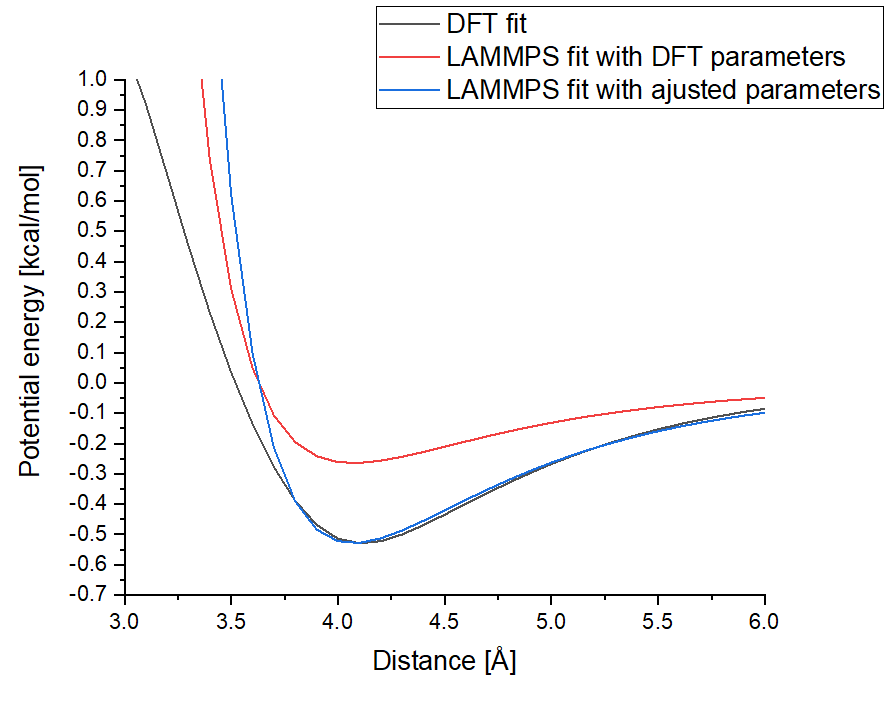
In the framework of my project, I am using the Lennard-Jones potential to describe the argon – silicon interactions for the simulation of argon bombardment of silicon. By fitting the Lennard-Jones potential 
to DFT data (Figure joined in annex), I have obtained the epsilon and sigma parameters for the argon – silicon interactions. The parameters give a well depth of 0.02298 eV (0.52854 kcal/mol). I am using the 5 May 2020 GitHub patch but this problem also appeared in previous LAMMPS versions.
In order to check the correctness of my parameters in LAMMPS, I output the potential energy as a function of distance for a pair of Ar-Si atoms (script in annex). To output the energy of my atoms, I am using the compute pe/atom and compute ke/atom commands. I run this script and change the distance between particles by increments, outputting the results of each compute in a file in order to reconstruct the data shown in the figure joined in annex, representing the obtained potential between my particles. When doing so, I can only tune two parameters of the lj/cut pair_style, which are the well depth and the zero crossing distance. After putting the aforementioned parameters into LAMMPS I obtain a shifted zero crossing distance and my depth well is divided by a factor 2!
In fact, to obtain the same well depth than the DFT data, I have to put 1.05712 kcal/mol for the well depth. Even tho the zero crossing distance seems to be shifted, the position of the potential’s minimum is correct, and it is the most relevant information for my case studies therefore I am not worrying too much about it.
My question is therefore: how are the well depth and the zero crossing distance handled by the lj/cut command, and why do I have to multiply by two the well depth in order to reproduce my DFT data? In the case the DTF would be wrong, the reproduced values in LAMMPS should still be fitting the DFT data, yet I have this factor two that I cannot explain on my own or after discussing it with my Ph.D. supervisor. Maybe the lj/cut command is not suitable for my specific case ? Anyone has already faced this issue ? Any help would be greatly appreciated.
Thank you in advance,
Best regards,
Grégoire DEFOORT, Ph.D.
Figure of the potential outputs:
(See attached file: Figure_Potentials.png)
Script Used:
3d reaxFF system
— initialisation ----------------------------
units real
#Real units: Kcal/mole - Angstroms - femtoseconds
dimension 3
boundary f f f
atom_style full
#atom_modify map array
print “Initialisation done…”
print “”
— variables ---------------------------------
variable time_step equal 1e-4
variable m_si equal 28.0855
variable m_ar equal 39.948
— atoms definition --------------------------
lattice none 1
region box block -10 10 -10 10 -10 10 units box
create_box 2 box
region silicon block -10 10 -10 10 -10 10 units box
#Fixed position Silicon particle
create_atoms 1 single 0 0 0
#Shifted position Argon particle
#The script loops and increases the z value of the Ar particle by 0.01 each step
create_atoms 2 single 0.0 0.0 0.01
print “Atoms defined”
print “”
— settings ----------------------------------
pair_style lj/cut 10
pair_coeff 1 2 1.05712 3.624 10
pair_coeff 1 1 0.98899999609 3.428 10
pair_coeff 2 2 0.69046 3.40776 10
mass 1 {m_si} mass 2 {m_ar}
neighbor 2.5 bin
neigh_modify every 1 delay 0 check yes
timestep ${time_step}
run_style verlet
— computes & thermo -------------------------
compute pe_Atom all pe/atom
compute ke_Atom all ke/atom
compute total_potential_energy all pe
compute total_kinetic_energy all ke
thermo 100
thermo_style custom step dt time temp density pe ke etotal press
dump 1 all custom 1 energy_Si-Ar.nve id element c_ke_Atom c_pe_Atom
dump_modify 1 element Si Ar format float “%20.13f”
thermo_modify lost warn norm yes flush yes
print “Settings done”
— run ---------------------------------------
print “Starting simulation”
run 1
print “Simulation ended”
“Pascal Brault” —02/06/2020 13:28:43—Hi Moreover,