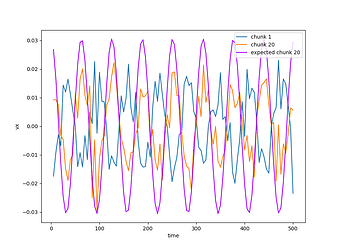
I am using LAMMPS version lammps-22Dec2022 on the CentOS operating system.
I intend to apply a sinusoidal deformation gamma_a * sin(omega * t) to the system, as shown in the figure below.
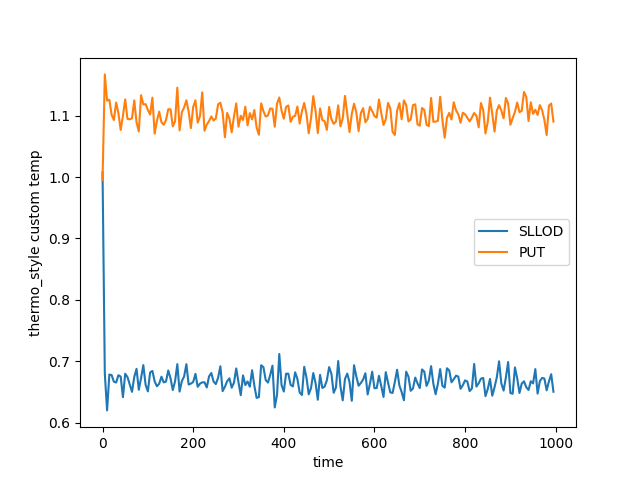
I utilized the fix deform wiggle ... remap v to induce deformation to the box. To apply this deformation to particles, I employed the fix nvt/sllod command.
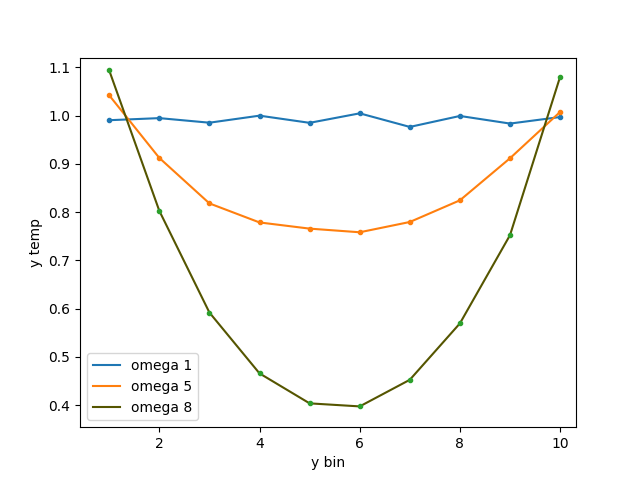
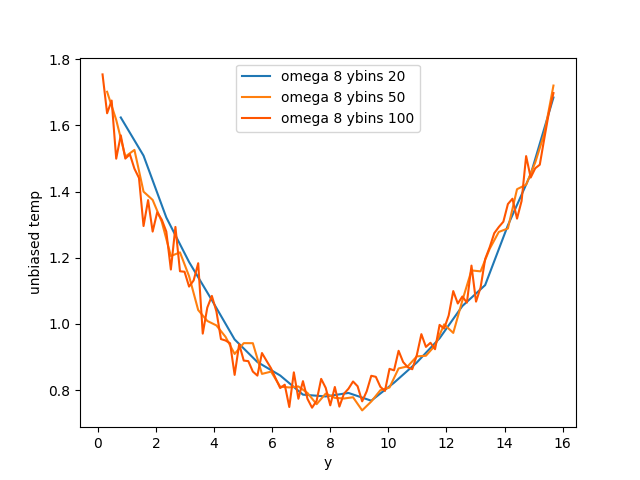
Next, the box is divided into 20 equal parts along the y direction, and the average x-direction velocities of particles in each part are calculated.
I expected the average x-direction velocity of particles at position y to be y * gamma_a * omega * cos(omega * t), with the maximum velocity at the top of the box (the twentieth part) and an average velocity of 0 at the bottom, with the same phase.
However, I observed a phase difference of pi, resulting in velocities being opposite to expectations. The velocity at the top of the box (the twentieth part) is 0.5 * y_max * gamma_a * omega * cos(omega * t) instead of y_max * gamma_a * omega * cos(omega * t).
This means that the x-direction velocity for the tenth part of the box is closer to 0.
I am aware of a similar issue in simple shear cases, where the solution involves adding the expected velocity gradient in the x-direction before shearing. However, this approach is not applicable to oscillatory scenarios.
I also noticed that a similar question was raised in this forum before, but a satisfactory solution was not provided. Additionally, LAMMPS does not have pre-existing examples of oscillatory shearing. I would like to ask if using fix deform wiggle ... remap v + fix nvt/sllod in LAMMPS can achieve oscillatory shear, as the nvt/sllod equation assumes a uniform velocity bias.
Below is my code.
variable strain equal 0.02
variable omega equal 0.1
units lj
dimension 3
boundary p p p
atom_style sphere
lattice fcc 1.38
region box block 0 11 0 11 0 11
create_box 2 box
create_atoms 1 box
group smaller_atoms id 1:19652:5
set group smaller_atoms type 2
change_box all triclinic
set type 1 mass 1
set type 2 mass 1
neighbor 1.0 multi
neigh_modify delay 0
comm_modify mode multi
pair_style lj/cut 2.5
pair_coeff 1 1 1.0 1.0 2.5
pair_coeff 2 2 0.5 0.88 2.5
pair_coeff 1 2 1.5 0.8 2.5
# start heat ################
velocity all create 5.0 4738964 dist gaussian rot yes
timestep 0.001
fix motion all nve
fix start_heat all langevin 5.0 5.0 $(100.0*dt) 347589123 zero yes
thermo 1000
thermo_style custom step temp epair etotal press vol pxy
run 50000
unfix start_heat
unfix motion
reset_timestep 0
# eq run #####################
velocity all zero linear
velocity all zero angular
velocity all scale 1.0
timestep 0.005
fix 1 all nvt temp 1 1 $(100.0*dt)
run 500000
unfix 1
# wiggle shear ###############
variable A equal v_strain*ly
variable T equal 2*PI/v_omega
fix 1 all deform 1 xy wiggle $(v_A) $(v_T) remap v units box
fix 2 all nvt/sllod temp 1.0 1.0 $(100.0*dt)
compute layers all chunk/atom bin/1d y center 0.05 units reduced
fix layers_vx all ave/chunk 20 50 1000 layers vx file profile_vx.txt
thermo_style custom step c_2_temp temp epair etotal press vol pxy
thermo 1000
run 100000
Thank you in advance.