Hello everyone,
I am currently using the force-matching (FM) method to derive classical force-fields. As me and the group I work with are new with it, I thought of sharing some thoughts on something I have been considering doing to get some opinion/criticism. (with roasting also totally allowed, if you feel like it)
So, basically I am trying to derive classical potentials for a coarse grained representation of a xtalline solid using FM. I am considering bonded and non-bonded potentials. Within FM, I am assuming in the case of the latter that the interactions in my system can be classically modelled by pairwise forces with the standard radial symmetry (which is not necessarily true actually). The mapping in hand has only one bead type (let’s call it 1). In my case, for bonded potentials, I have only one angle type and one bond type.
My reference force data comes from an atomistic simulation ran with an already-existing classical model reported in the literature. For what is worth it, I am not using the original first-ever published force-matching formalism by Ercolessi and Adams but rather one that was used by Voth et al (Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching | The Journal of Chemical Physics | AIP Publishing) some time later, being, in essence, the difference simply that in the latter case an overdetermined system of equations is assembled to seek for optimal force-fields of a given form.
When working with force-matching, some people say that it is okay to consider the forces of a given contribution as being 0 in the non-sampled regions (for example, in the case of the 1-1 interaction, the non-sampled regions would be the values of distances 1-1 that are never explored, which we can find out by checking an RDF of a reference system). Others say that it is necessary to have sampling throughout the entire continuous range of distances one is trying to derive a force-field for. Particularly, I tend to believe in the latter case because I think that my chances of converging to potentials that are physically meaningful are larger (fundamentally, force-matching, in its mathematical formalism, is somewhat free to deliver phisically weird potentials).
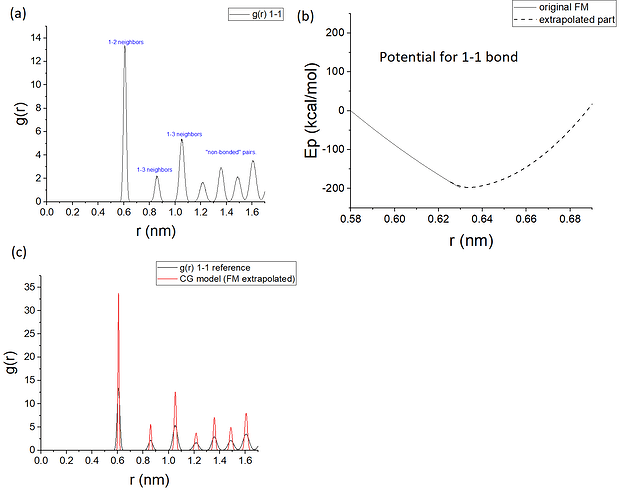
My system (a crystalline solid) has actually some non-sampled regions: as it can be seen in figure (a), the peaks of the reference RDF for the mapping are not merged to one another. Some people that worked with FM for solids sampled microstates in the molten state and therefore had data to fit forces in regions of the rij distances that are not sampled in the xtalline state. I, however, cannot do such thing in the sense that, not only the material I am studying is not supposed to melt in “real life”, but also, even if I was to try to force it to happen computationally, my bonded force-fields in the AA model have harmonic-like shape, which I doubt would allow me to compromise the xtall structure. What I can do is to simulate it at a high temperature thermodynamic state and, as I have a larger degree of motion, the RDF peaks merge and therefore I would have data in the entire range of r 1-1 in which the non-bonded potential is supposed to act. This is also something that other people seem to have done.
By doing this, I successfully managed to get the peaks corresponding to non-bonded pairs in figure (a) to merge a little as they become wider. Yet, when I did the FM, I ended up getting potentials that seem a “little weird” to me and to other potentials I’ve seen reported in the literature (at least for the bonded contributions). I mean, I dont doubt that the FM protocol was carried out correctly in the sense that the potential for bonds + angles + pairwise 1-1 can in theory be a most optimal solution within FM mathematically speaking. But physically speaking, it is weird… for example, my bonded potentials are all repulsive. If this is the case, it should not be difficult to have bonded atoms straying too far away then, unless somehow the other contributions were able to balance it out. Indeed, as it turns out, there is no such balance and my simulation ends up collapsing.
It could be that I cannot derive potentials for my system using force-matching. It could also be (maybe more likely) that the assumption of modelling interactions with these “isotropic” pairwise potentials are valid. I am still to investigate other potential forms and symmetries. But another thing that I thought I could do is to do an extrapolation of the bonded potentials in the way shown in figure (b) for the potential for bonds. I mean, I am cheating in the sense that by extrapolating the potentials in this way I will be forcing the bonded contributions into respecting the xtal structure that I am expecting for my system. Not to mention that I will be introducing forces that will not really have come from force-matching - although some people sometimes use hybrid approaches, so it’s not like they are deriving “pure force matching” potentials is compulsory either. At the same time, as the extrapolated part of the potential fights to bring back the pairs to the sampled regions (part of the potential derived via FM), I will not be allowing my system to sample regions that should be unsampled in my extrapolation-methodology. In fact, I will be colaborating for a potential that is able to reproduce the structure also as a consequence of ther harmonic shape I am using for the extrapolation (see figure (c), which corresponds to reference and model structural data at 300K). What do you guys think?